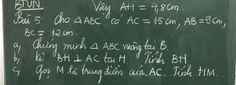a: Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔABC vuông tại B
b: \(BH=\dfrac{9\cdot12}{15}=7.2\left(cm\right)\)
a, Ta có : \(AC^2=AB^2+BC^2\Leftrightarrow225=144+81\)* đúng *
Vậy tam giác ABC vuông tại B
b, Ta có : \(S_{ABC}=\dfrac{1}{2}BH.AC;S_{ABC}=\dfrac{1}{2}AB.BC\Rightarrow BH.AC=AB.BC\)
\(\Rightarrow BH=\dfrac{AB.BC}{AC}=\dfrac{36}{5}cm\)
c, Theo định lí Pytago tam giác ABH vuông tại H
\(AH=\sqrt{AB^2-BH^2}=\dfrac{27}{5}cm\)
Xét tam giác ABC vuông tại B có M là trung điểm AC
=> BM = AM = CM = AC/2 = 15/2
=> HM = AM - AH = \(\dfrac{21}{10}\)