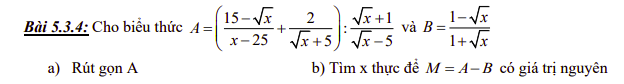a) \(A=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\left(đk:x\ge0,x\ne25\right)\)
\(=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}.\dfrac{\sqrt{x}-5}{\sqrt{x}+1}=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}.\dfrac{\sqrt{x}-5}{\sqrt{x}+1}=\dfrac{1}{\sqrt{x}+1}\)
b) \(M=A-B=\dfrac{1}{\sqrt{x}+1}-\dfrac{1-\sqrt{x}}{1+\sqrt{x}}=\dfrac{1-1+\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}}{\sqrt{x}+1}=1-\dfrac{1}{\sqrt{x}+1}\in Z\)
\(\Rightarrow\sqrt{x}+1\inƯ\left(1\right)=\left\{1;-1\right\}\)
Do \(\sqrt{x}\ge0\)
\(\Rightarrow x\in\left\{0\right\}\)
Đúng 3
Bình luận (0)