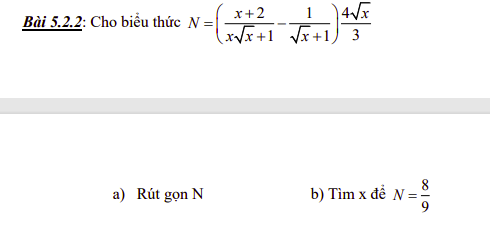ĐK: x ≥ 0
\(N=\left(\dfrac{x+2}{x\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right).\dfrac{4\sqrt{x}}{3}=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}.\dfrac{4\sqrt{x}}{3}=\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}.\dfrac{4\sqrt{x}}{3}=\dfrac{1}{x-\sqrt{x}+1}.\dfrac{4\sqrt{x}}{3}=\dfrac{4\sqrt{x}}{3x-3\sqrt{x}+3}\)
b) \(N=\dfrac{8}{9}\)
\(\Rightarrow\dfrac{4\sqrt{x}}{3x-3\sqrt{x}+3}=\dfrac{8}{9}\)
\(\Rightarrow\dfrac{\sqrt{x}}{x-\sqrt{x}+1}=\dfrac{2}{3}\)
\(\Rightarrow3\sqrt{x}-2x+2\sqrt{x}-2=0\)
\(\Rightarrow5\sqrt{x}-2x-2=0\)
\(\Rightarrow-2x+4\sqrt{x}+\sqrt{x}-2=0\)
\(\Rightarrow-2\sqrt{x}\left(\sqrt{x}-2\right)+\left(\sqrt{x}-2\right)=0\)
\(\Rightarrow\left(\sqrt{x}-2\right)\left(-2\sqrt{x}+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{4}\end{matrix}\right.\left(t.m\right)\)