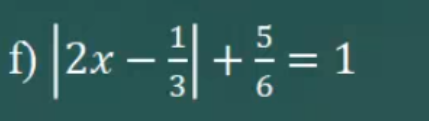\(\left|2x-\dfrac{1}{3}\right|+\dfrac{5}{6}=1\)
\(\Leftrightarrow\left|2x-\dfrac{1}{3}\right|=\dfrac{1}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{1}{3}=\dfrac{1}{6}\left(x\ge\dfrac{1}{6}\right)\\2x-\dfrac{1}{3}=-\dfrac{1}{6}\left(x< \dfrac{1}{6}\right)\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\left(tm\right)\\x=\dfrac{1}{12}\left(tm\right)\end{matrix}\right.\)
`|2x-1/3|+5/6=1`
`|2x-1/3|=1/6`
TH1: `2x-1/3>=0 <=> x >= 1/6`
`2x-1/3=1/6`
`2x=1/2`
`x=1/4`
TH2: `2x-1/3<0<=>x<1/6`
`2x-1/3=-1/6`
`2x=1/6`
`x=1/12`
Vậy `x=1/4; x=1/12`.
\(\Leftrightarrow\left|2x-\dfrac{1}{3}\right|=\dfrac{1}{6}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{1}{3}=\dfrac{1}{6}\\2x-\dfrac{1}{3}=-\dfrac{1}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{1}{3}+\dfrac{1}{6}=\dfrac{1}{2}\\2x=\dfrac{1}{3}-\dfrac{1}{6}=\dfrac{1}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=\dfrac{1}{12}\end{matrix}\right.\)