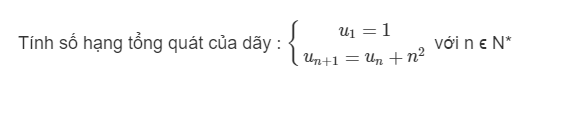Ta cần tìm các hệ số a;b;c sao cho:
\(u_{n+1}-a\left(n+1\right)^3-b\left(n+1\right)^2-c\left(n+1\right)=u_n-an^3-bn^2-cn\)
\(\Rightarrow u_{n+1}=u_n+3an^2+\left(3a+2b\right)n+\left(a+b+c\right)\)
Đồng nhất hệ số với \(u_{n+1}=u_n+n^2\)
\(\Rightarrow\left\{{}\begin{matrix}3a=1\\3a+2b=0\\a+b+c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{3}\\b=-\dfrac{1}{2}\\c=\dfrac{1}{6}\end{matrix}\right.\)
\(\Rightarrow u_{n+1}-\dfrac{1}{3}\left(n+1\right)^3+\dfrac{1}{2}\left(n+1\right)^2-\dfrac{1}{6}\left(n+1\right)=u_n-\dfrac{1}{3}n^3+\dfrac{1}{2}n^2-\dfrac{1}{6}n\)
Đặt \(v_n=u_n-\dfrac{1}{3}n^3+\dfrac{1}{2}n^2-\dfrac{1}{6}n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-\dfrac{1}{3}+\dfrac{1}{2}-\dfrac{1}{6}=1\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{1}{3}n^3+\dfrac{1}{2}n^2-\dfrac{1}{6}n=1\)
\(\Rightarrow u_n=\dfrac{1}{3}n^3-\dfrac{1}{2}n^2+\dfrac{1}{6}n+1\)
\(u_1=1\)
\(u_2=u_1+1\)
\(u_3=u_2+1\)
...
\(u_{n-1}=u_{n-2}+1\)
\(u_n=u_{n-1}+1\)
Cộng vế theo vế các đẳng thức trên ta được:
\(u_1+u_2+...+u_n=n+\left(u_1+u_2+...+u_{n-1}\right)\)
\(\Rightarrow u_n=n\)