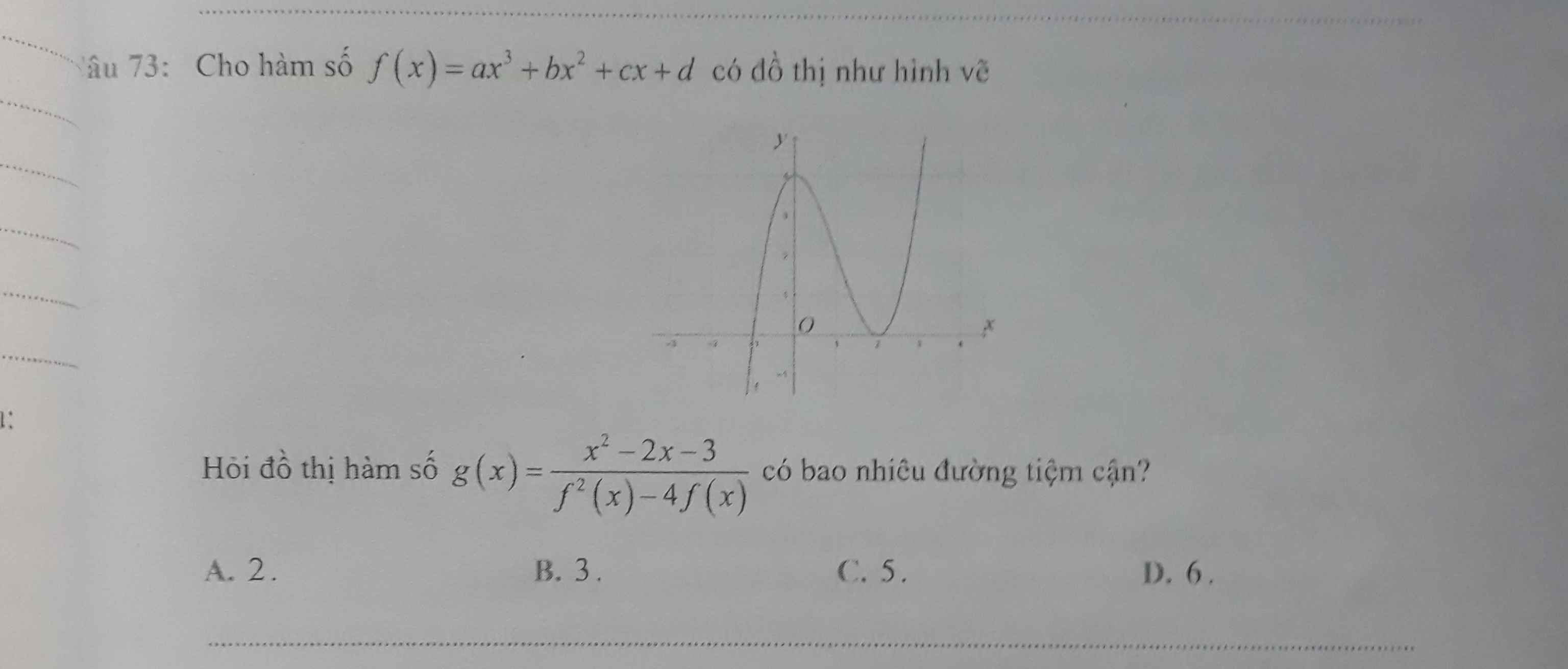
141.
Có 2 cách: 1 là dựng đồ thị \(\left|f\left(x\right)\right|\) bằng cách lấy đối xứng phần bên dưới trục hoành lên (sẽ hơi dài)
2 là chia trường hợp và xài luôn đồ thị \(f\left(x\right)\) có sẵn:
\(\left|f\left(x\right)\right|=1\Rightarrow\left[{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-1\end{matrix}\right.\)
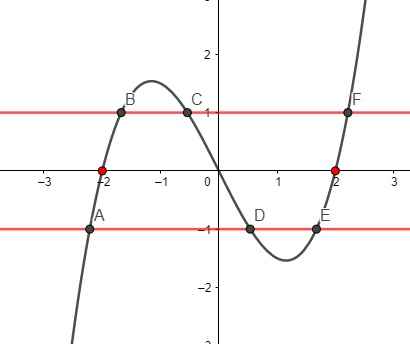
Vẽ 2 đường thẳng \(y=1\) và \(y=-1\) lên cùng đồ thị \(f\left(x\right)\), ta thấy mỗi đường cắt đồ thị tại 3 điểm \(\Rightarrow\) tổng cộng có 6 giao điểm. Nhưng trong 6 giao điểm có 2 điểm nằm ngoài [-2;2] là A và F nên chỉ có 4 giao điểm thuộc [-2;2]
Hay pt \(\left|f\left(x\right)\right|=1\) có 4 nghiệm trên [-2;2]
140.
Hoàn toàn tương tự câu 141
\(\left|f\left(x\right)\right|=1\Rightarrow\left[{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-1\end{matrix}\right.\)
Vẽ 2 đường thẳng \(y=1\) và \(y=-1\) lên cùng hệ trục, ta thấy \(y=1\) cắt đồ thị tại 2 điểm, nhưng 2 điểm này đều nằm ngoài đoạn [-2;2] \(\Rightarrow\) loại
\(y=-1\) cắt đồ thị tại 2 điểm đều nằm trong [-2;2] thỏa mãn
Vậy \(\left|f\left(x\right)\right|=1\) có 2 nghiệm trên [-2;2] (cả 4 đáp án đều ko chính xác, phương trình này có 4 nghiệm là đúng, nhưng có 4 nghiệm trên [-2;2] là sai)