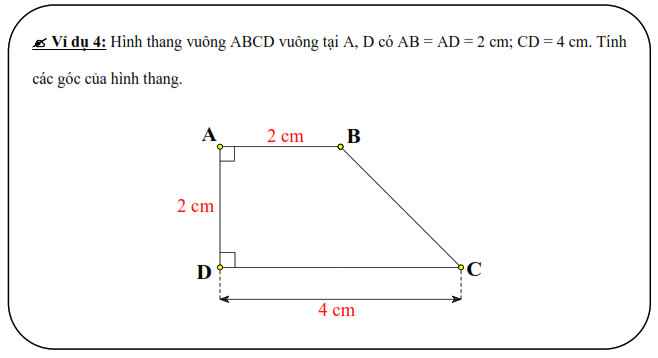
Gọi M là trung điểm CD \(\Rightarrow DM=CM=\dfrac{1}{2}CD=2\left(cm\right)\)
\(\Rightarrow AB=DM\)
Mà \(AB||DM\Rightarrow ABMD\) là hình bình hành (tứ giác có cặp cạnh đối song song và bằng nhau)
Do \(\widehat{A}=90^0\Rightarrow ABMD\) là hcn
\(\Rightarrow BM\perp CD\) hay tam giác BCM vuông tại M (1)
Cũng do ABMD là hcn \(\Rightarrow BM=AD=2\left(cm\right)\)
\(\Rightarrow BM=CM\) (2)
(1);(2) \(\Rightarrow\Delta BCM\) vuông cân tại M
\(\Rightarrow\widehat{C}=45^0\)
\(\Rightarrow\widehat{B}=180^0-45^0=135^0\)