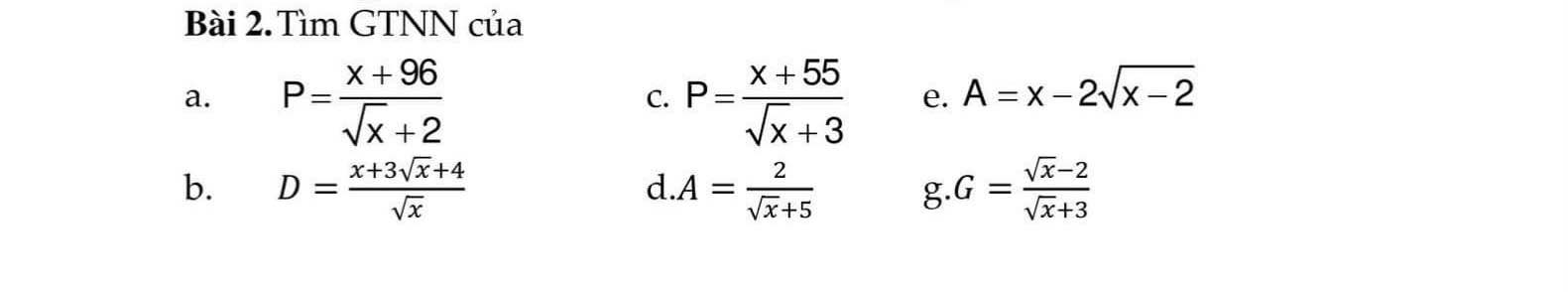a)\(P=\dfrac{x+96}{\sqrt{x}+2}=\dfrac{\left(x-4\right)+100}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{100}{\sqrt{x}+2}=\left(\sqrt{x}+2+\dfrac{100}{\sqrt{x}+2}\right)-4\ge2\sqrt{\left(\sqrt{x}+2\right).\dfrac{100}{\sqrt{x}+2}}-4=16\)
Dấu "=" xảy ra khi \(\sqrt{x}+2=\dfrac{100}{\sqrt{x}+2}\Leftrightarrow x=64\)
Vậy \(P_{min}=16\)
b)Đk: x>0
\(D=\dfrac{x+3\sqrt{x}+4}{\sqrt{x}}=\sqrt{x}+3+\dfrac{4}{\sqrt{x}}=\left(\sqrt{x}+\dfrac{4}{\sqrt{x}}\right)+3\ge2\sqrt{\sqrt{x}.\dfrac{4}{\sqrt{x}}}+3=7\)
Dấu "=" xảy ra khi \(\sqrt{x}=\dfrac{4}{\sqrt{x}}\Leftrightarrow x=4\)
Vậy \(D_{min}=7\)
c)Đk: \(x\ge0\)
\(P=\dfrac{x+55}{\sqrt{x}+3}=\dfrac{\left(x-9\right)+64}{\sqrt{x}+3}=\sqrt{x}-3+\dfrac{64}{\sqrt{x}+3}\)\(=\left(\sqrt{x}+3+\dfrac{64}{\sqrt{x}+3}\right)-6\ge2\sqrt{\left(\sqrt{x}+3\right).\dfrac{64}{\sqrt{x}+3}}-6=10\)
Dấu "=" xảy ra khi \(\sqrt{x}+3=\dfrac{64}{\sqrt{x}+3}\Leftrightarrow x=25\)
Vậy \(P_{min}=10\)
d) \(x\ge0\)
\(A=\dfrac{2}{\sqrt{x}+5}\)
A đạt GTNN khi \(\sqrt{x}+5\) đạt GTLN \(\Leftrightarrow\sqrt{x}\) đạt GTLN (Không tồn tại x để \(\sqrt{x}\) đạt GTLN)
Vậy không tồn tại giá trị nhỏ nhất của A( chỉ có GTLN)
e) Đk: \(x\ge2\)
\(A=x-2\sqrt{x-2}=\left(x-2\right)-2\sqrt{x-2}+1+1=\left(\sqrt{x-2}-1\right)^2+1\ge1\)
Dấu "=" xảy ra khi \(\sqrt{x-2}-1=0\Leftrightarrow x=3\) (tm)
Vậy \(A_{min}=1\)
g) ĐK: \(x\ge0\)
\(G=\dfrac{\sqrt{x}-2}{\sqrt{x}+3}=1-\dfrac{5}{\sqrt{x}+3}\)
Có \(\sqrt{x}+3\ge3;\forall x\ge0\) \(\Rightarrow\dfrac{5}{\sqrt{x}+3}\le\dfrac{5}{3}\)\(\Rightarrow1-\dfrac{5}{\sqrt{x}+3}\ge1-\dfrac{5}{3}\)\(\Leftrightarrow G\ge-\dfrac{2}{3}\)
Dấu "=" xảy ra khi x=0
Vậy \(G_{min}=-\dfrac{2}{3}\)
\(P=\sqrt{x}-2+\dfrac{4}{\sqrt{x}+2}\)
\(P=\sqrt{x}+2+\dfrac{4}{\sqrt{x}+2}-4\)
Áp dụng BDT Cô-si ta có:
\(\sqrt{x}+2+\dfrac{4}{\sqrt{x}+2}\ge2\sqrt{\sqrt{x}+2.\dfrac{4}{\sqrt{x}+2}}\)
P ≥ \(2\sqrt{4}-4\)
MinP=0 ⇔\(\sqrt{x}+2=\dfrac{4}{\sqrt{x}+2}\)
\(\Leftrightarrow\left(\sqrt{x}+2\right)^2=4\)
\(\Leftrightarrow\sqrt{x}+2=2\)
\(\Leftrightarrow x=0\)
c) Ta có: \(P=\dfrac{x+55}{\sqrt{x}+3}\)
nên \(P=\dfrac{x-9+64}{\sqrt{x}+3}=\sqrt{x}-3+\dfrac{64}{\sqrt{x}+3}\)
\(\Leftrightarrow P=\left(\sqrt{x}+3+\dfrac{64}{\sqrt{x}+3}\right)+6\)
\(\Leftrightarrow P\ge2\cdot8+6=16+6=22\)
Dấu '=' xảy ra khi \(\sqrt{x}+3=8\)
\(\Leftrightarrow\sqrt{x}=5\)
hay x=25