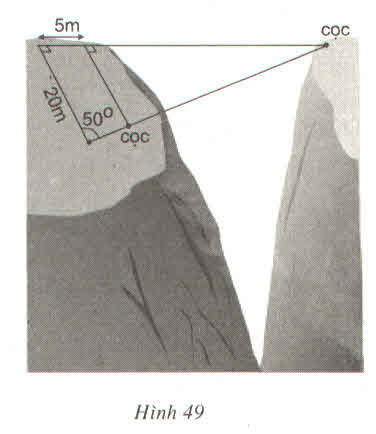
Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)
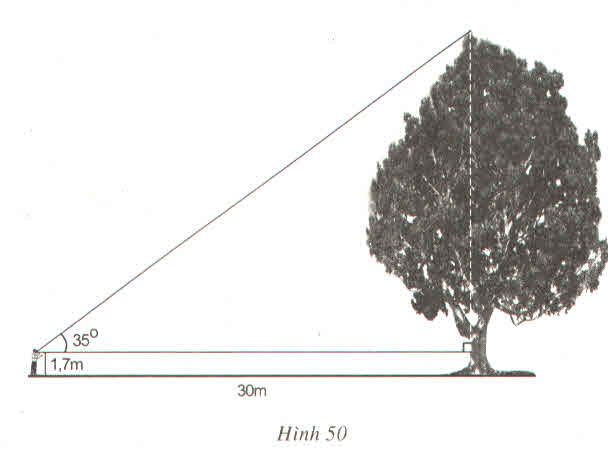
Tính chiều cao của cây trong hình 50 (làm tròn đến dm)
Đáp án và hướng dẫn giải bài 40: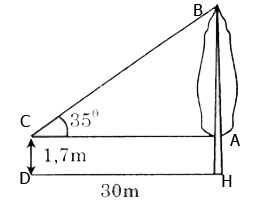
Chiều cao của cây là:
BH = BA + Ah = AC tgC + AH
=30.tg350 + 1,7 ≈ 22,7 m
Trả lời bởi Nhật Linh
Tam giác ABC vuông tại C có \(AC=2cm,BC=5cm,\widehat{BAC}=x,\widehat{ABC}=y\)
Dùng các thông tin sau (nếu cần) để tìm \(x-y\) :
\(\sin23^036'\approx0,4\)
\(\cos66^024'\approx0,4\)
\(tg21^048'\approx0,4\)
Ta có tgy =2/5 = 0,4 ⇒ tgy= tg21048′ ⇒ y= 21048′
x = 900 – 21048′ = 68012′
x – y = 68012′ -21048′ = 46024′
Trả lời bởi Nhật LinhỞ một cái thang dài 3m, người ta ghi : "Để đảm bảo an toàn khi dùng thang phải đặt thang này tạo với mặt đất 1 góc có độ lớn từ \(60^0\) đến \(70^0\)". Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết : Khi dùng thang đó chân thang phải cách tường khoảng bao nhiêu mét để đảm bảo an toàn ?
Vậy khi dùng thang, phải đặt thang cách chân tường một khoảng từ 1,03m đến 1,5 m để đảm bảo an toàn.
Trả lời bởi Phan Thùy LinhĐố :
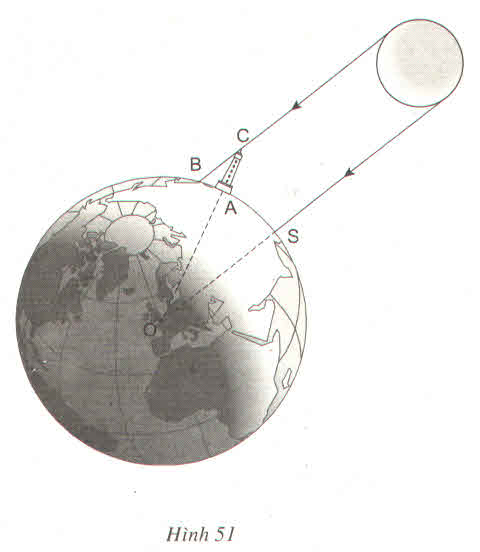
Vào khoảng năm 200 trước Công nguyên, Ơ - ra - tô - xten, một nhà toán học và thiên văn học Hi lạp đã ước lượng được "chu vi" của Trái Đất (chu vi đường xích đạo) nhờ hai quan sát sau :
1) Một ngày trong năm, ông để ý thấy Mặt Trời chiếu thẳng các đáy giếng ở thành phố Xy-en (nay gọi là Át - xu - an), tức là tia sáng chiếu thẳng đứng
2) Cùng lúc đó ở thành phố A - lếch - xăng - đri - a cách Xy - en 800km, một tháp cao 25m có bóng trên mặt đất dài 3,1m
Từ hai quan sát trên, em hãy tính xấp xỉ "chu vi" của Trái Đất
(Trên hình 51, điểm S tượng trưng cho thành phố Xy - en, điểm A tượng trưng cho thành phố A - lếch - xăng - đri - a, bóng của tháp trên mặt đất được coi là đoạn thẳng AB
Trong hình bên, ta có thể coi các tia sáng mặt trời chiếu song song, cung AB quá nhỏ (3,1dm) nên xem là đoạn thẳng. Khi đó ta vẽ được hình với giả thiết cung AS = 800km, AC = 25m, AB = 3,1m, SO // CB. Hãy tính chu vi của đường tròn tâm O, bán kính SO bằng công thức c = 800.(360/a)
Hãy tính x và y trong các hình sau :
a)Áp dụng hệ thức lượng trong tam giác ta có:
72 = y(x+y)
52 = x(x+y)
=> (x+y)2=52+72=25+49=74
Do x,y là độ dài cạnh tam giác nên x>0 y>0
=>x+y=\(\sqrt{74}\)
=>x = \(25:\sqrt{74}=\dfrac{25\sqrt{74}}{74}\)
y = \(49:\sqrt{74}=\dfrac{49\sqrt{74}}{74}\)
b)Áp dụng hệ thức lượng trong tam giác ta có:
y(x+y) = 142 = 196
x+y=16(giả thiết)
=> y = 196:16 = 12,25
=> x = 16-12,25=3,75
Trả lời bởi Xuân Tuấn TrịnhHãy tính \(\sin\alpha\) và \(tg\alpha\) nếu :
a) \(\cos\alpha=\dfrac{5}{13}\)
b) \(\cos\alpha=\dfrac{15}{17}\)
c) \(\cos\alpha=0,6\)
a: \(\sin a=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\)
\(\tan a=\dfrac{12}{5}\)
b: \(\sin a=\sqrt{1-\left(\dfrac{15}{17}\right)^2}=\dfrac{8}{17}\)
\(\tan a=\dfrac{8}{15}\)
c: \(\sin a=\sqrt{1-0.6^2}=0.8\)
nên \(\tan a=\dfrac{4}{3}\)
Trả lời bởi Nguyễn Lê Phước ThịnhHãy đơn giản biểu thức :
a) \(1-\sin^2\alpha\)
b) \(\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha\cos^2\alpha\)
c) \(\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)\)
d) \(tg^2\alpha-\sin^2\alpha.tg^2\alpha\)
e) \(1+\sin^2\alpha+\cos^2\alpha\)
g) \(\cos^2\alpha+tg^2\alpha.\cos^2\alpha\)
h) \(\sin\alpha-\sin\alpha.\cos^2\alpha\)
i) \(tg^2\alpha\left(2\cos^2\alpha+\sin^2\alpha-1\right)\)
đáp án :
a) \(cos^2\alpha\)
b) 1
c) \(sin^2\alpha\)
d) \(sin^2\alpha\)
e) 2
g) 1
h) \(sin^3\alpha\)
i) \(sin^2\alpha\)
Trả lời bởi Mysterious Person
Trong một tam giác với các cạnh có độ dài 6, 7, 9, kẻ đường cao đến cạnh lớn nhất. Hãy tìm độ dài đường cao này và các đoạn thẳng mà nó định ra trên cạnh lớn nhất đó ?
Hãy tìm độ dài cạnh đáy của một tam giác cân, nếu đường cao kẻ xuống đáy có độ dài là 5 và đường cao kẻ xuống cạnh bên có độ dài là 6 ?
Kí hiệu như hình vẽ. Theo hệ thức giữa cạnh và góc của tam giác vuông: Trong tam giác vuông ABC:
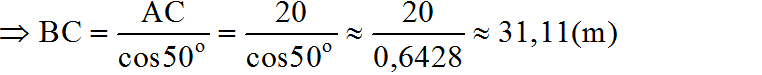
Trả lời bởi Lưu Hạ Vy