a) Vẽ đường tròn tâm O, bán kính 2cm.
b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a.
c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O; r).
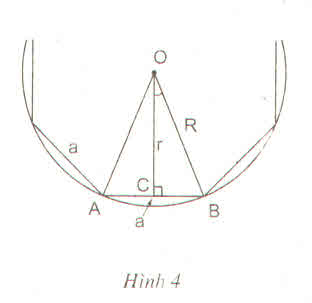
a) Vẽ tam giác đều ABC cạnh a = 3 cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O ; R).
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).
Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.
Hình a.
Gọi ai là cạnh của đa giác đều i cạnh.
a) a6= R (vì OA1A2 là tam giác đều)
Cách vẽ: vẽ đường tròn (O;R). Trên đường tròn ta đặt liên tiếp các cung 
, 
,..., 
mà căng cung có độ dài bằng R. Nối A1 với A2, A2 với A3,…,A6 với A1 ta được hình lục giác đều A1A2A3A4A5A6 nội tiếp đường tròn
b) Hình b
Trong tam giác vuông OA1A2: a2 = R2 + R2 = 2R2 => a4 = R√2
Cách vẽ như ở bài tập 61.
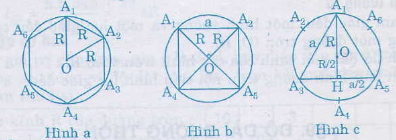
c) Hình c
A1H = R + =
A3H =
A1A3 = a
Trong tam giác vuông A1HA3 ta có: A1H2 = A1A32 – A3H2.
Từ đó = a2 -
.
=> a2 = 3R2 => a = R√3
Cách vẽ như câu a) hình a.
Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác A1A3A5 như trên hình c
Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho số đo cung AB = 60o; số đo cung BC = 90o và số đo cung CD = 120o.
a) Tứ giác ABCD là hình gì?
b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác ABCD theo R.
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3
Vẽ hình vuông ABCD tâm O rồi vẽ tam giác đều có một đỉnh là A và nhận O làm tâm. Nêu cách vẽ ?
Vẽ đường tròn tâm O bán kính R = 2cm rồi vẽ hình tám cạnh đều nội tiếp đường tròn (O; 2cm). Nêu cách vẽ ?
Cho một đa giác đều n cạnh có độ dài mỗi cạnh là a. Hãy tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp đa giác đều đó ?
Hướng dẫn : Tính \(\widehat{COB}\) rồi tính \(\sin\widehat{COB}\) và \(tg\widehat{COB}\), từ đây tính được R và r
a) Vẽ một lục giác đều ABCDEG nội tiếp đường tròn bán kính 2cm rồi vé hình 12 cạnh đều AIBJCKDEMGN nội tiếp đường tròn đó. Nêu cách vẽ :
a) Tính độ dài cạnh AI
b) Tính bán kính r của đường tròn nội tiếp hình AIBJCKDEMGN
Hướng dẫn : Áp dụng các công thức ở bài 46
a) Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính 3cm
b) Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính 3cm
Tính cạnh của hình 8 cạnh đều theo bán kính R của đường tròn ngoại tiếp :
Hướng dẫn :
Cách 1 : Áp dụng công thức :
\(a=2R\sin\dfrac{180^0}{n}\)
Cách 2 : Tính trực tiếp
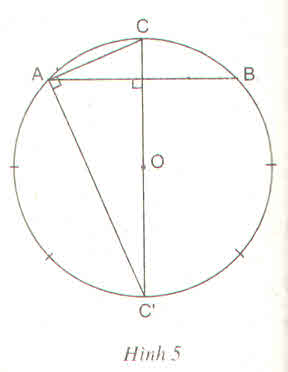
Vẽ dây AB là cạnh của một hình vuông nội tiếp đường tròn (O), gọi C là điểm chính giữa của cung nhỏ AB. Khi đó CA là cạnh của hình tám cạnh đều nội tiếp. Hãy tính CA trong tam giác vuông CAC' (h.5)
a) Chọn điểm O làm tâm , mở compa có độ dài 2cm vẽ đường tròn tâm O, bán kính 2cm: (O; 2cm)
Vẽ bằng eke và thước thẳng.
b) Vẽ đường kính AC và BD vuông góc với nhau. Nối A với B, B với C, C với D, D với A ta được tứ giác ABCD là hình vuông nội tiếp đường tròn (O;2cm)
c) Vẽ OH ⊥ AD
OH là bán kính r của đường tròn nội tiếp hình vuông ABCD.
r = OH = AH.
r2 + r2 = OA2 = 22 => 2r2 = 4 => r = √2 (cm)
Vẽ đường tròn (O;√2cm). Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh
Trả lời bởi ¨°o.O♫♀¤♪ Zin Phan ♪¤♂♫O...