Chứng minh rằng vi phân \(dy\) và số gia \(\Delta y\) của hàm số \(y=ax+b\) trùng nhau ?
Chứng minh rằng với \(\left|x\right|\) rất bé so với \(a>0\left(\left|x\right|\le a\right)\) ta có :
\(\sqrt{a^2+x}\approx a+\dfrac{x}{2a};\left(a>0\right)\)
Áp dụng công thức trên, hãy tính gần đúng các số sau :
a) \(\sqrt{146}\)
b) \(\sqrt{34}\)
c) \(\sqrt{120}\)
Tìm vi phân của hàm số sau :
\(y=\dfrac{x+2}{x-1}\)
Tìm \(\dfrac{d\left(\tan x\right)}{d\left(\cot x\right)}\)
Tìm vi phân của hàm số sau :
\(y=\sin^2x\)
dy = d(sin2x) = (sin2x)’dx = cosx.2sinxdx = sin2xdx.
Trả lời bởi Nguyễn Lê Phước ThịnhTìm vi phân của hàm số sau :
\(y=\dfrac{1}{x^2}\)
Tìm \(dy\) biết :
a) \(y=\tan^2x\)
b) \(y=\dfrac{\cos x}{1-x^2}\)
a) \(dy=d\left(tan^2x\right)=\left(tan^2x\right)'dx=2tanx.\left(tanx\right)'dx=\dfrac{2tanx}{cosx}dx\)
b) \(dy=d\left(\dfrac{cosx}{1-x^2}\right)=\left(\dfrac{cosx}{1-x^2}\right)'dx=\dfrac{\left(cosx\right)'.\left(1-x^2\right)-cosx\left(1-x^2\right)'}{\left(1-x^2\right)^2}dx=\dfrac{\left(x^2-1\right).sinx+2xcosx}{\left(1-x^2\right)^2}=dx\)
Trả lời bởi Quốc ĐạtTìm vi phân của các hàm số sau :
a) \(y=\dfrac{\sqrt{x}}{a+b}\) (a, b là các hằng số)
b) \(y=\left(x^2+4x+1\right)\left(x^2-\sqrt{x}\right)\)
a) \(dy=d\left(\dfrac{\sqrt{x}}{a+b}\right)=\left(\dfrac{\sqrt{x}}{a+b}\right)dx=\dfrac{1}{2\left(a+b\right)\sqrt{x}}dx\)
b) \(dy=d\left(x^2+4x+1\right)\left(x^2-\sqrt{x}\right)=\left[\left(2x+4\right)\left(x^2-\sqrt{x}\right)+\left(x^2+4x+1\right)\left(2x-\dfrac{1}{2\sqrt{x}}\right)\right]dx\)
Trả lời bởi Quốc ĐạtCho hàm số :
\(f\left(x\right)=x^3-2x+1\)
Hãy tính \(\Delta f\left(1\right),df\left(1\right)\) và so sánh chúng nếu :
a) \(\Delta x=1\)
b) \(\Delta x=0,1\)
c) \(\Delta x=0,01\)
Tìm vi phân của hàm số sau :
\(y=\dfrac{\tan\sqrt{x}}{\sqrt{x}}\)
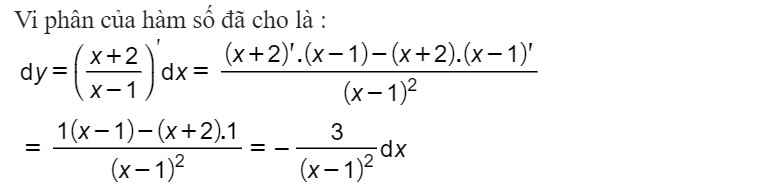
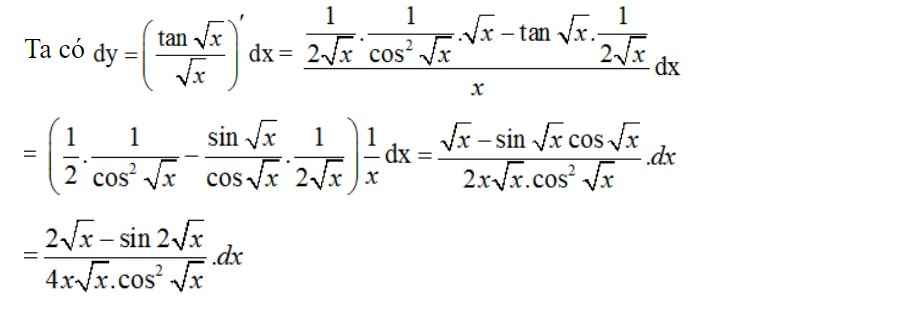
y = ax + b ⇒ y′ = a và dy = adx = aΔx;
Δy = a(x + Δx) + b − [ax + b] = aΔx..
Vậy dy = Δy.
Trả lời bởi Nguyễn Lê Phước Thịnh