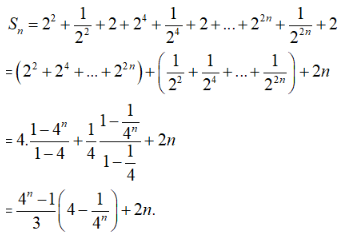Tính tổng \(S_n=\left(2+\dfrac{1}{2}\right)^2+\left(4+\dfrac{1}{4}\right)^2+...+\left(2^n+\dfrac{1}{2^n}\right)^2\).
\(S=\dfrac{4^n-1}{3}\left(4-\dfrac{1}{4^n}\right)+n\).\(S=\dfrac{1-4^n}{3}\left(4-\dfrac{1}{4^n}\right)+2n\).\(S=\dfrac{4^n-1}{3}\left(\dfrac{1}{4^n}-4\right)+n\).\(S=\dfrac{4^n-1}{3}\left(4-\dfrac{1}{4^n}\right)+2n\).Hướng dẫn giải: