Cho hình bình hành \(ABCD\), điểm \(F\) nằm trên cạnh \(BC\). Tia \(AF\) cắt \(BD\) và \(DC\) lần lượt ở \(E\) và \(G\). Chọn khẳng định sai?
\(\Delta BFE\) đồng dạng với \(\Delta DAE\).\(\Delta DEG\) đồng dạng với \(\Delta BEA\).\(\Delta BFE\) đồng dạng với \(\Delta DEA\).\(\Delta DGE\) đồng dạng với \(\Delta BAE\).Hướng dẫn giải: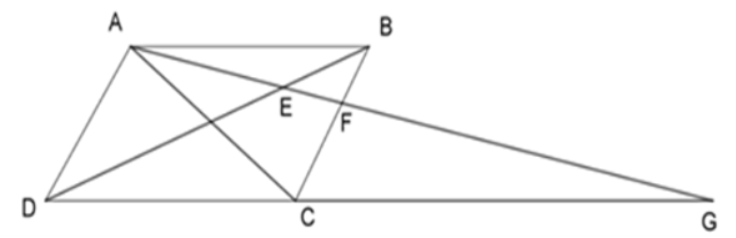
Do \(ABCD\) là hình bình hành nên \(AB\)//\(CD\) ; \(AD\)//\(BC\)
\(\Rightarrow\widehat{ADE}=\widehat{FBE}\) (so le trong) ; \(\widehat{ABE}=\widehat{EDG}\) (so le trong)
+) Xét \(\Delta BFE\) và \(\Delta DAE\) có:
\(\widehat{ADE}=\widehat{FBE}\) (cmt)
\(\widehat{AED}=\widehat{FEB}\) (đối đỉnh)
Suy ra \(\Delta BFE\) đồng dạng với \(\Delta DAE\)
+) Xét \(\Delta DGE\) và \(\Delta BAE\) có:
\(\widehat{ABE}=\widehat{EDG}\) (cmt)
\(\widehat{AEB}=\widehat{GED}\) (đối đỉnh)
Suy ra \(\Delta DGE\) đồng dạng với \(\Delta BAE\)
Hay \(\Delta DEG\) đồng dạng với \(\Delta BEA\).
