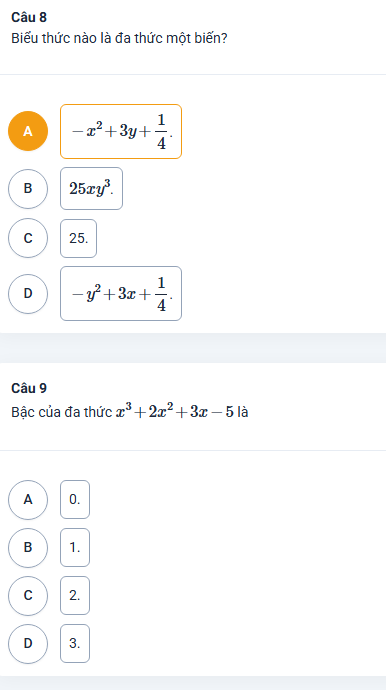
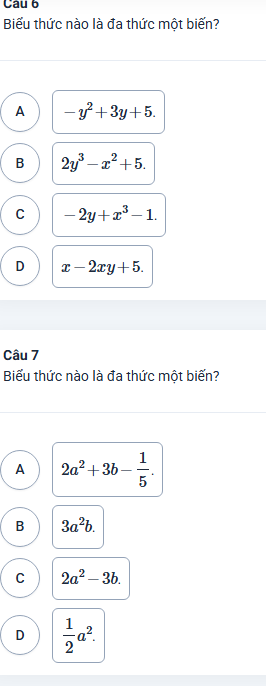
Cứu em với ạ:<<
Cứu em với ạ:<<

 giúp với
giúp với
Bài 4:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x+y-z}{3+5-7}=\dfrac{9}{1}=9\)
=>\(\left\{{}\begin{matrix}x=9\cdot3=27\\y=9\cdot5=45\\z=9\cdot7=63\end{matrix}\right.\)
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}=\dfrac{2x+3y+4z}{2\cdot5+3\cdot3+4\cdot2}=\dfrac{54}{10+9+8}=2\)
=>\(\left\{{}\begin{matrix}x=2\cdot5=10\\y=2\cdot3=6\\z=2\cdot2=4\end{matrix}\right.\)
Bài 5:
a: Xét ΔAOB và ΔAOC có
AO chung
OB=OC
AB=AC
Do đó: ΔAOB=ΔAOC
b: ΔAOB=ΔAOC
=>\(\widehat{ABO}=\widehat{ACO}\)
ΔAOB=ΔAOC
=>\(\widehat{OAB}=\widehat{OAC}\)
=>AO là phân giác của góc BAC
c: Ta có: OB=OC
=>O nằm trên đường trung trực của BC(1)
ta có: IB=IC
=>I nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OI là đường trung trực của BC
d: Ta có: AB=AC
=>A nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,O,I thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H
a) Chứng minh tam giác ABH=tam giác ACH
b) Kẻ HD vuông góc với AB (D thuộc AB) ; HE vuông góc với AC (E thuộc AC). Chứng minh tam giác ADE cân và DE // BC
c) Gọi giao điểm của DH và AC là I. Chứng minh: IE+AD>2DH
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
Đúng 0
Bình luận (0)
Cho M=4an+2-3an+2an+2-8an-5an+2+2an(n∈Z)
Giá trị lớn nhất của a để M=0 là
\(M=4\cdot a^{n+2}-3a^n+2\cdot a^{n+2}-8a^n-5a^{n+2}+2a^n\)
\(=\left(4\cdot a^{n+2}+2\cdot a^{n+2}-5\cdot a^{n+2}\right)+\left(-3a^n-8a^n+2a^n\right)\)
\(=a^{n+2}-9a^n=a^n\cdot\left(a^2-9\right)\)
Để M=0 thì \(a^n\left(a^2-9\right)=0\)
=>\(\left[{}\begin{matrix}a^n=0\\a^2-9=0\end{matrix}\right.\Leftrightarrow a\in\left\{0;3;-3\right\}\)
=>Giá trị lớn nhất của a để M=0 là a=3
Đúng 0
Bình luận (0)

 giúp tớ với ạ
giúp tớ với ạ
Bài 1:
\(C\left(m\right)=-1-7m^5+2m^2-9m^3+\sqrt{2}\cdot m+4m^3-2m^5\)
\(=\left(-7m^5-2m^5\right)+\left(-9m^3+4m^3\right)+2m^2+m\sqrt{2}-1\)
\(=-9m^5-5m^3+2m^2+m\sqrt{2}-1\)
bậc là 5
Các hệ số là -9;-5;2;\(\sqrt{2}\);-1
Bài 2:
a: Khi x=3 và y=2 thì \(C=\left(3-2\right)^2+2\cdot3-2+5\)
=1+6-2+5
=7-2+5
=5+5
=10
b: KHi x=-1 và y=2 thì \(B=5\cdot\left(-1\right)^2-4\cdot\left(-1\right)\cdot2+7\)
=5+8+7
=5+15=20
Đúng 0
Bình luận (0)
Câu 3: (3,0 điểm). Cho
vuông tại A, đường phân giác của góc B cắt AC tại
D.Trên cạnh BC lấy điểm E sao cho BA = BE.
a) Chứng minh
b) So sánh AD và DC
c) Gọi F là giao điểm của hai đường thẳng BA và ED. Chứng minh BD vuông góc
với FC.
Cho tam giác ABC có B = 70 độ, C = 30 độ kẻ AH vuông góc với BC ( H thuộc BC )
a.So sánh AC và AB, AH và AC
b.Trên tia AH lấy điểm D sao cho H là trung điểm cuả đoạn thẳng AD. c/m tam giác ADC đều
a) Ta có :
\(AC\) là cạnh đối diện \(\widehat{B}=70^o\)
\(AB\) là cạnh đối diện \(\widehat{C}=30^o< 70^o\)
\(\Rightarrow AC>AB\)
Tam giác \(AHC\) vuông tại \(H\) (\(AH\) là đường cao) có :
\(AH\) là cạnh góc vuông; \(AC\) là cạnh huyền
\(\Rightarrow AH< AC\)
b) Ta có :
\(H\) là trung điểm \(AD\left(gt\right)\)
\(\Rightarrow HC\) là đường trung tuyến \(\Delta ADC\)
mà \(HC\) là cũng đường cao (\(AH\) là đường cao)
\(\Rightarrow\Delta ADC\) là tam giác cân tại \(C\)
mà \(\widehat{HAC}=90^0-30^0=60^o\) (\(\Delta AHC\) vuông tại \(H\)) hay \(\widehat{DAC}=60^0\)
\(\Rightarrow\Delta ADC\) là tam giác đều
\(\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
Tính Tổng các hệ số của đa thức Q(x)(x2−2x+2)2019.(x2−3x+3)2020Giúp e với ạ
Đọc tiếp
Tính Tổng các hệ số của đa thức
Giúp e với ạ![]()
\(Q\left(1\right)=\left(1^2-2\cdot1+2\right)^{2019}\cdot\left(1^2-3\cdot1+3\right)^{2020}\)
\(=\left(1-2+2\right)^{2019}\cdot\left(1-3+3\right)^{2020}\)
=1
=>Tổng các hệ số của đa thức Q(x) là 1
Đúng 0
Bình luận (0)