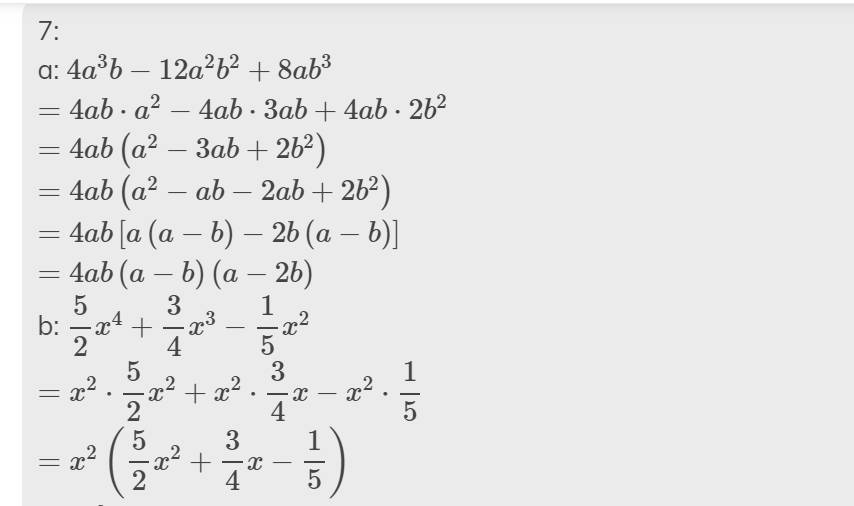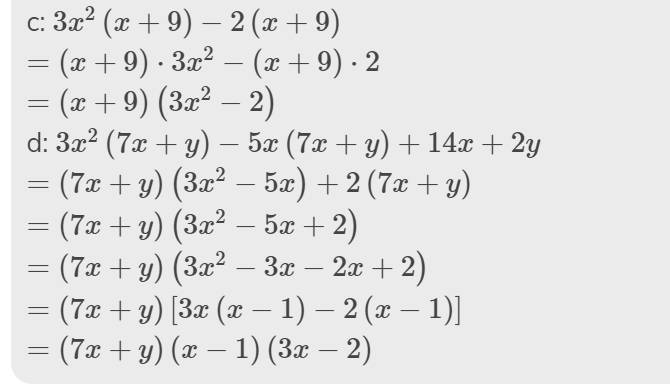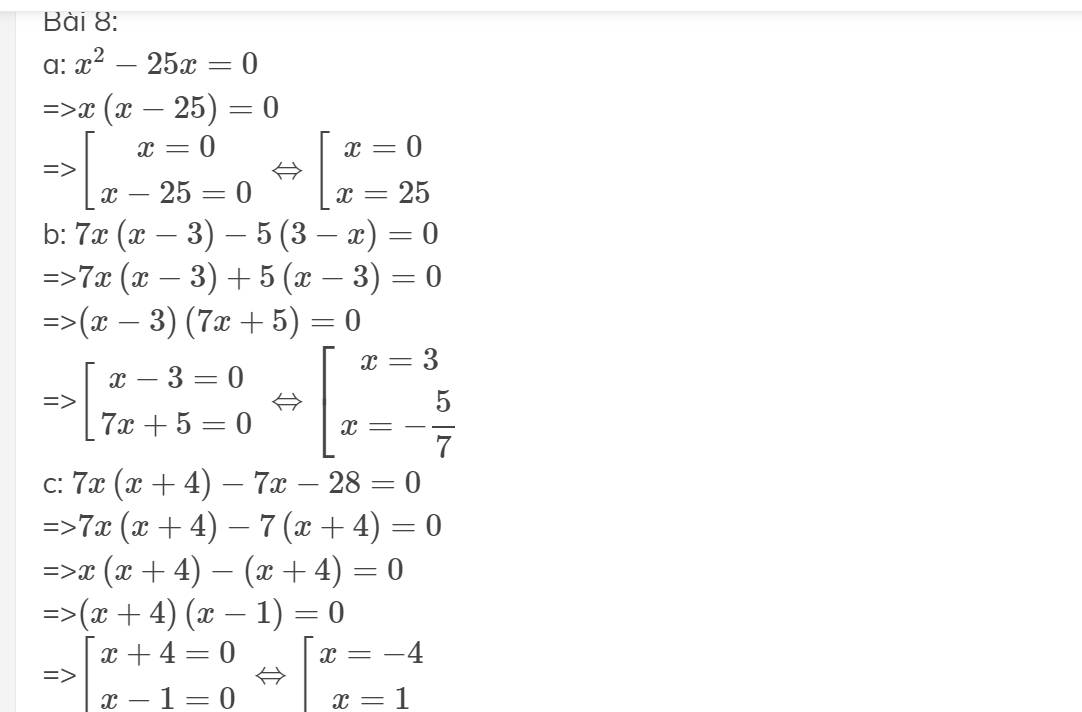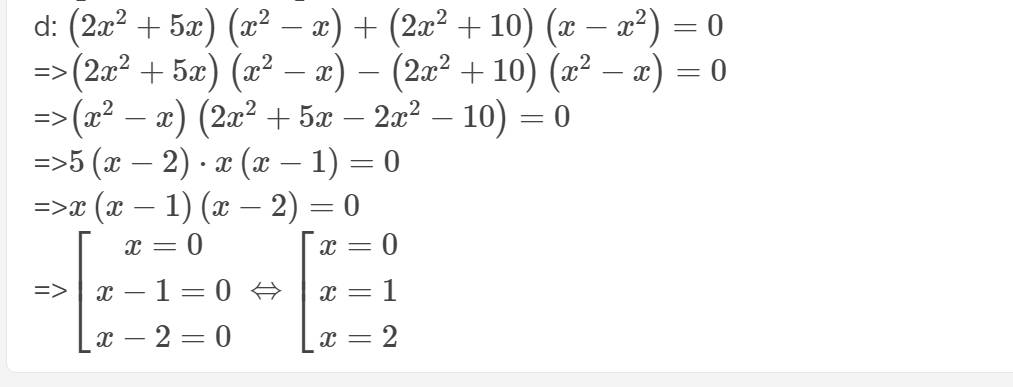(\(\dfrac{3x-2}{x-2}\) - \(\dfrac{x}{x+2}\)+ \(\dfrac{4}{x^2-4}\)) : \(\dfrac{x+3}{x^2-4}\)
Phép nhân và phép chia các đa thức
\(\left(\dfrac{3x-2}{x-2}-\dfrac{x}{x+2}+\dfrac{4}{x^2-4}\right):\dfrac{x+3}{x^2-4}\left(x\ne\pm2;x\ne-3\right)\)
\(=\left[\dfrac{\left(3x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{4}{\left(x-2\right)\left(x+2\right)}\right]\cdot\dfrac{x^2-4}{x+3}\)
\(=\dfrac{3x^2+4x-4-x^2+2x+4}{x^2-4}\cdot\dfrac{x^2-4}{x+3}\)
\(=\dfrac{2x^2+6x}{x+3}\)
\(=\dfrac{2x\left(x+3\right)}{x+3}=2x\)
Đúng 1
Bình luận (0)
phân tích đa thức 9x2- 4y2 thành nhân tử ta được
\(9x^2-4y^2\)
\(=\left(3x\right)^2-\left(2y\right)^2\)
\(=\left(3x-2y\right)\left(3x+2y\right)\)
Đúng 0
Bình luận (0)
thực hiện phép chia :
[ 10x^2 (x+2)^3 -8x^3(x+2)^2+4x(x+2)^3] : 2x(x+2)^2\(\dfrac{10x^2\left(x+2\right)^3-8x^3\left(x+2\right)^2+4x\left(x+2\right)^3}{2x\left(x+2\right)^2}\)
\(=\dfrac{10x^2\left(x+2\right)^3}{2x\left(x+2\right)^2}-\dfrac{8x^3\left(x+2\right)^2}{2x\left(x+2\right)^2}+\dfrac{4x\left(x+2\right)^3}{2x\left(x+2\right)^2}\)
\(=\dfrac{2x\cdot\left(x+2\right)^2\cdot5x\cdot\left(x+2\right)}{2x\left(x+2\right)^2}-\dfrac{2x\cdot\left(x+2\right)^2\cdot4x^2}{2x\left(x+2\right)^2}+\dfrac{2x\left(x+2\right)^2\cdot2\cdot\left(x+2\right)}{2x\left(x+2\right)^2}\)
\(=5x\left(x+2\right)-4x^2+2\left(x+2\right)\)
\(=5x^2+10x-4x^2+2x+4\)
\(=x^2+12x+4\)
Đúng 2
Bình luận (0)
thực hiện phép chia :
Xem chi tiết
( x - y )^7: ( y - x )^6
\(\left(x-y\right)^7:\left(y-x\right)^6\left(dk:x\ne y\right)\)
\(=\left(x-y\right)^7:\left(x-y\right)^6\)
\(=x-y\)
Đúng 1
Bình luận (0)
( x - y )^7: ( y - x )^6
\((x-y)^7:(y-x)^6(dk:x\ne y)\)
\(=\dfrac{\left(x-y\right)^7}{\left(y-x\right)^6}=\dfrac{\left(x-y\right)^7}{\left(x-y\right)^6}=x-y\)
Đúng 3
Bình luận (0)
c: \(x^3-3x^2+x-3=0\)
=>\(\left(x^3-3x^2\right)+\left(x-3\right)=0\)
=>\(x^2\left(x-3\right)+\left(x-3\right)=0\)
=>\(\left(x-3\right)\left(x^2+1\right)=0\)
mà \(x^2+1>=1>0\forall x\)
nên x-3=0
=>x=3
d: \(\left(3x+5\right)^2=\left(x-7\right)^2\)
=>\(\left(3x+5\right)^2-\left(x-7\right)^2=0\)
=>\(\left(3x+5+x-7\right)\left(3x+5-x+7\right)=0\)
=>\(\left(4x-2\right)\left(2x+12\right)=0\)
=>\(\left[{}\begin{matrix}4x-2=0\\2x+12=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-6\end{matrix}\right.\)
Đúng 1
Bình luận (0)
 chi ttết ạ cảm ơn nhiều
chi ttết ạ cảm ơn nhiều
c: \(25-a^2+2ab-b^2\)
\(=25-\left(a^2-2ab+b^2\right)\)
\(=5^2-\left(a-b\right)^2\)
\(=\left(5-a+b\right)\left(5+a-b\right)\)
d: \(\dfrac{1}{27}a^3y-8b^3y\)
\(=y\left(\dfrac{1}{27}a^3-8b^3\right)\)
\(=y\left[\left(\dfrac{1}{3}a\right)^3-\left(2b\right)^3\right]\)
\(=y\left(\dfrac{1}{3}a-2b\right)\left[\left(\dfrac{1}{3}a\right)^2+\dfrac{1}{3}a\cdot2b+\left(2b\right)^2\right]\)
\(=y\left(\dfrac{1}{3}a-2b\right)\left(\dfrac{1}{9}a^2+\dfrac{2}{3}ab+4b^2\right)\)
e: \(a^3-a+b^3-b\)
\(=\left(a^3+b^3\right)-\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)-\left(a+b\right)\)
\(=\left(a+b\right)\left(a^2-ab+b^2-1\right)\)
g: \(5x^4y^2+20x^3y^2+20x^2y^2\)
\(=5x^2y^2\cdot x^2+5x^2y^2\cdot4x+5x^2y^2\cdot4\)
\(=5x^2y^2\left(x^2+4x+4\right)=5x^2y^2\left(x+2\right)^2\)
Đúng 1
Bình luận (0)
 chi tiết nhất
chi tiết nhất
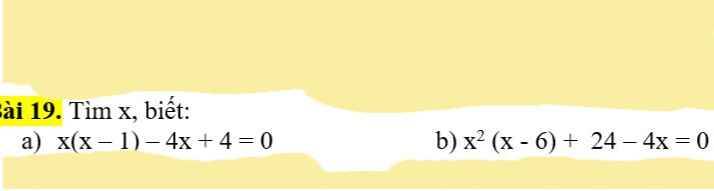
a: \(x\left(x-1\right)-4x+4=0\)
=>\(x\left(x-1\right)-\left(4x-4\right)=0\)
=>\(x\left(x-1\right)-4\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(x-4\right)=0\)
=>\(\left[{}\begin{matrix}x-1=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
b: \(x^2\left(x-6\right)+24-4x=0\)
=>\(x^2\left(x-6\right)-\left(4x-24\right)=0\)
=>\(x^2\left(x-6\right)-4\left(x-6\right)=0\)
=>\(\left(x-6\right)\left(x^2-4\right)=0\)
=>\(\left(x-6\right)\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-6=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=2\\x=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
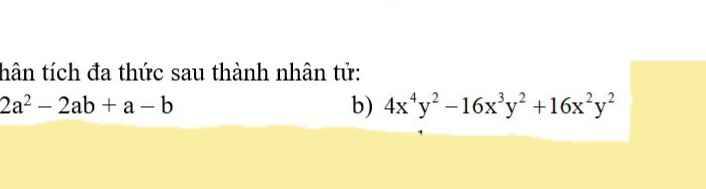 chi tiết
chi tiết
a: \(2a^2-2ab+a-b\)
\(=\left(2a^2-2ab\right)+\left(a-b\right)\)
\(=2a\left(a-b\right)+\left(a-b\right)\)
\(=\left(a-b\right)\left(2a+1\right)\)
b: \(4x^4y^2-16x^3y^2+16x^2y^2\)
\(=4x^2y^2\cdot x^2-4x^2y^2\cdot4x+4x^2y^2\cdot4\)
\(=4x^2y^2\left(x^2-4x+4\right)\)
\(=4x^2y^2\left(x-2\right)^2\)
Đúng 2
Bình luận (0)
 chi tiết giúp với ai cứu tui sắp đi học rôdi
chi tiết giúp với ai cứu tui sắp đi học rôdi