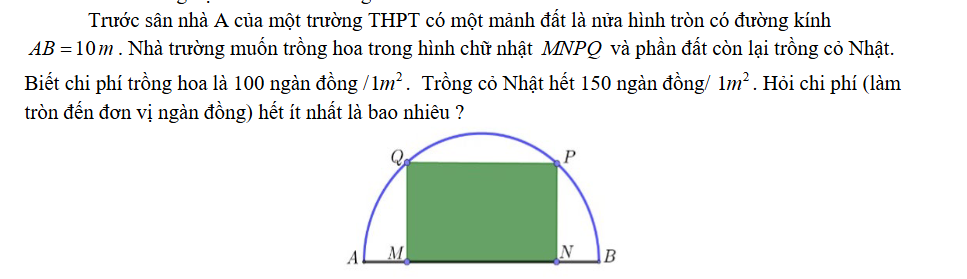
Bán kính \(r=\dfrac{AB}{2}=5\left(m\right)\)

Diện tích nửa hình tròn \(S=\dfrac{1}{2}\pi r^2=\dfrac{25\pi}{2}\left(m^2\right)\)

Đặt \(MN=x\left(0< x< 10\right);MQ-y\)

\(MNPQ\) là hình chữ nhật nội tiếp nửa đường tròn, ta có:

\(OM=\dfrac{x}{2};OQ=y\)

Áp dụng Pitago cho tam giác vuông \(OMQ:\dfrac{x^2}{4}+y^2=25\)

\(\Rightarrow y=\sqrt{25-\dfrac{x^2}{4}}\)

\(S_{MNPQ}=xy=x\sqrt{25-\dfrac{x^2}{4}}\left(m^2\right)\)

\(S_{cỏ}=\dfrac{25\pi}{2}-xy\)

Tổng chi phí: 

\(C=C_{hoa}+C_{cỏ}=100000xy+150000\left[\dfrac{25\pi}{2}-xy\right]=1875000\pi-50000xy\)

Để \(C_{min}\Rightarrow xy\left(max\right)\)

Áp dụng bất đẳng thức Cauchuy cho \(\dfrac{x^2}{4};25-\dfrac{x^2}{4}\)

\(\dfrac{x^2}{4}+\left(25-\dfrac{x^2}{4}\right)\ge2\sqrt{\dfrac{x^2}{4}.\left(25-\dfrac{x^2}{4}\right)}\)

\(\Rightarrow25\ge x\sqrt{25-\dfrac{x^2}{4}}=xy\)

Dấu"=" xảy ra khi \(\dfrac{x^2}{4}=25-\dfrac{x^2}{4}\Rightarrow x=5\sqrt{2}\)

\(\Rightarrow y=\sqrt{25-\dfrac{50}{4}}=\dfrac{5\sqrt{2}}{2}\)

\(\Rightarrow xy=5\sqrt{2}.\dfrac{5\sqrt{2}}{2}=25\)

\(\Rightarrow C_{min}=1875000\pi-50000xy\approx4637500\approx4638000\left(đồng\right)\)

Vấn đề bạn cần hỏi chắc chỉ nằm ở câu d

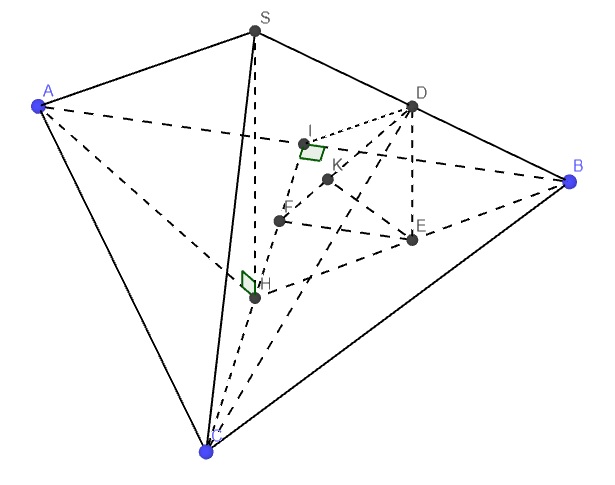
Ko cần quan tâm điểm G, gọi D là trung điểm của SB thì \(G\in CD\) nên \(d\left(SA;CG\right)=d\left(SA;CD\right)\)

Mặt khác \(DI||SA\) (đường trung bình) nên 

\(SA||\left(CDI\right)\Rightarrow d\left(SA;CD\right)=d\left(A;\left(CDI\right)\right)=d\left(B;\left(CDI\right)\right)\) do I là trung điểm AB

Gọi E là trung điểm BH \(\Rightarrow DE||SH\) (đường trung bình) \(\Rightarrow DE\perp\left(ABC\right)\)

Từ E kẻ EF vuông góc CI, kẻ EK vuông góc DF \(\Rightarrow DK=d\left(E;\left(CDI\right)\right)=\dfrac{1}{2}d\left(B;\left(CDI\right)\right)\)

\(EF=\dfrac{1}{2}BI=\dfrac{1}{4}AB=\dfrac{\sqrt{3}}{4}\) (đường trung bình)

\(DE=\dfrac{1}{2}SH=\dfrac{\sqrt{21}}{8}\)

\(\Rightarrow d\left(SA;CG\right)=2DK=2.\dfrac{EF.DE}{\sqrt{EF^2+DE^2}}=\dfrac{\sqrt{399}}{38}\) (có tính sai ko nhỉ)

\(\left(\alpha\right)\perp\left(\beta\right)\Rightarrow\left(2m-1\right)m+\left(-3m\right)\left(m-1\right)+2\cdot4=0\)

\(\Rightarrow-m^2+2m+8=0\)

\(\Rightarrow\left[{}\begin{matrix}m=4\\m=-2\end{matrix}\right.\)

Vậy m = 4 hoặc m = -2 

\(\left(\alpha\right):\left(2m-1\right)x-3my+2z+3=0\Rightarrow\overrightarrow{n_1}=\left(2m-1;-3m;2\right)\)

\(\left(\beta\right):mx+\left(m-1\right)y+4z-5=0\Rightarrow\overrightarrow{n_2}=\left(m;m-1;4\right)\)

\(\left(\alpha\right)\perp\left(\beta\right)\Rightarrow\overrightarrow{n_1}.\overrightarrow{n_2}=0\)

\(\Leftrightarrow\left(2m-1\right)m-3m\left(m-1\right)+2.4=0\)

\(\Leftrightarrow2m^2-m-3m^2+3m+8=0\)

\(\Leftrightarrow m^2-2m-8=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=-2\\m=4\end{matrix}\right.\)

Vậy với \(m=-2\cup m=4\) thỏa mãn yêu cầu đề bài

Do \(b;c;d\) đôi một khác nhau và nằm trong tập \(\left\{1;2;...9\right\}\), ta cần đếm số cách chọn ba số khác nhau theo thứ tự.

Chọn số thứ nhất \(b\): Có \(9\) cách chọn

Chọn số thứ hai \(c\) \(\left(c\ne b\right)\): Có \(8\) cách chọn

Chọn số thứ ba \(d\) \(\left(d\ne b;c\right)\): Có \(7\) cách chọn

Vì thứ tự chọn không quan trọng (chúng ta chỉ quan tâm đến tập hợp các số, không phải hoán vị của chúng), nên phải chia cho số cách sắp xếp 3 phần tử, tức là \(3!=6\)

Vậy số bộ số \(b;c;d\) thỏa mãn đề bài là \(\dfrac{9.8.7}{6}=84\left(cách.chọn\right)\)

a) \(V_1=\pi\int\limits^4_0\left(\sqrt{x}-0\right)^2dx=\pi\int\limits^4_0xdx\RightarrowĐúng\)

b) \(V_2=\pi\int\limits^4_0\left(\dfrac{1}{2}\sqrt{x}-0\right)^2dx=\pi\int\limits^4_0\dfrac{1}{4}xdx\Rightarrow Sai\)

c) \(V_1=\pi\left[\dfrac{x^2}{2}\right]^4_0=8\pi\)

\(V_2=\pi\left[\dfrac{x^2}{8}\right]^4_0=2\pi\)

\(\Rightarrow V_1-V_2=6\pi\Rightarrow Sai\)

d) Thể tích của vật thể A là:

\(V_A=\pi\int\limits^4_0\left(\left(\sqrt{x}\right)^2-\left(\dfrac{1}{2}\sqrt{x}\right)^2\right)dx=\pi\int\limits^4_0\left(x-\dfrac{1}{4}x\right)dx\)

\(\Rightarrow V_A=\pi\int\limits^4_0\dfrac{3}{4}xdx=\left[\dfrac{3x^2}{8}\right]^4_0=6\pi\approx18,84\left(cm^3\right)\Rightarrow Sai\)

e ra bằng -6 rồi ạ, kh phải giúp nữa đâu ạa

a) Gọi trục tọa độ \(Oxyz:A\left(0;0;0\right);B\left(a;0;0\right);C\left(a;a;0\right);D\left(0;a;0\right);S\left(\dfrac{a}{2};0;\dfrac{a\sqrt{3}}{2}\right)\)

\(\overrightarrow{SB}=\left(\dfrac{a}{2};0;-\dfrac{a\sqrt{3}}{2}\right);\overrightarrow{SD}=\left(-\dfrac{a}{2};a;-\dfrac{a\sqrt{3}}{2}\right)\)

\(\Rightarrow\overrightarrow{n\left(SBD\right)}=\left[\overrightarrow{SB}.\overrightarrow{SD}\right]=\left(\dfrac{a^2}{2};\dfrac{a^2\sqrt{3}}{2};\dfrac{a^2\sqrt{3}}{2}\right)=\left(1;\sqrt{3};\sqrt{3}\right)\)

\(\Rightarrow\left(SBD\right):\left(x-a\right)+\sqrt{3}\left(y-0\right)+\sqrt{3}\left(z-0\right)=0\)

\(\Rightarrow\left(SBD\right):x+\sqrt{3}y+\sqrt{3}z-a=0\)

\(d\left(A;\left(SBD\right)\right)=\dfrac{\left|0+\sqrt{3}.0+\sqrt{3}.0-a\right|}{\sqrt{1+3+3}}=\dfrac{a\sqrt{7}}{7}\)

b) \(G\) là trọng tâm \(\Delta SAB\Rightarrow G\left(\dfrac{0+a+\dfrac{a}{2}}{3};\dfrac{0+0+0}{3};\dfrac{0+0+\dfrac{a\sqrt{3}}{2}}{3}\right)=\left(\dfrac{a}{2};0;\dfrac{a\sqrt{3}}{6}\right)\)

\(M\) là trung điểm \(SC\Rightarrow M\left(\dfrac{a+\dfrac{a}{2}}{2};\dfrac{a+0}{2};\dfrac{0+\dfrac{a\sqrt{3}}{2}}{2}\right)=\left(\dfrac{3a}{4};\dfrac{a}{2};\dfrac{a\sqrt{3}}{4}\right)\)

\(N\) là trung điểm \(SD\Rightarrow N\left(\dfrac{0+\dfrac{a}{2}}{2};\dfrac{a+0}{2};\dfrac{0+\dfrac{a\sqrt{3}}{2}}{2}\right)=\left(\dfrac{a}{4};\dfrac{a}{2};\dfrac{a\sqrt{3}}{4}\right)\)

\(\overrightarrow{GM}=\left(\dfrac{a}{4};\dfrac{a}{2};\dfrac{a\sqrt{3}}{12}\right);\overrightarrow{GN}=\left(-\dfrac{a}{4};\dfrac{a}{2};\dfrac{a\sqrt{3}}{12}\right)\)

\(\Rightarrow\overrightarrow{n\left(GMN\right)}=\left[\overrightarrow{GM}.\overrightarrow{GN}\right]=\left(\dfrac{a^2}{4};-\dfrac{a^2\sqrt{3}}{24};0\right)=\left(1;-\dfrac{\sqrt{3}}{6};0\right)\)

\(\Rightarrow\left(GMN\right):\left(x-\dfrac{a}{2}\right)-\dfrac{\sqrt{3}}{6}\left(y-0\right)+0.\left(z-\dfrac{a\sqrt{3}}{6}\right)=0\)

\(\Rightarrow\left(GMN\right):x-\dfrac{\sqrt{3}}{6}y-\dfrac{a}{2}=0\)

\(d\left(S;\left(GMN\right)\right)=\dfrac{\left|\dfrac{a}{2}-\dfrac{\sqrt{3}}{6}.0-\dfrac{a}{2}\right|}{\sqrt{1+\dfrac{1}{12}}}=0\)

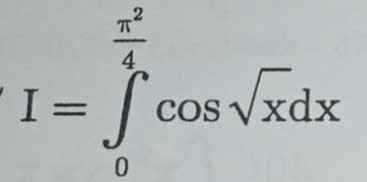
Đặt \(t=\sqrt{x}\Rightarrow\left\{{}\begin{matrix}x=t^2\\dx=2dt\end{matrix}\right.\)

\(x=0\Rightarrow t=0\)

\(x=\dfrac{\pi^2}{4}\Rightarrow t=\dfrac{\pi}{2}\)

\(\Rightarrow I=2\int\limits^{\dfrac{\pi}{2}}_0tcos\left(t\right)dt\)

Đặt \(u=t;dv=costdt\Rightarrow du=dt;v=sint\)

\(\Rightarrow\int udv=uv-\int vdu\) (Tích phân từng phần)

\(\Rightarrow I=2\left[tsint|^{\dfrac{\pi}{2}}_0-\int\limits^{\dfrac{\pi}{2}}_0sintdt\right]\)

\(\Rightarrow I=2\left[\dfrac{\pi}{2}.sin\dfrac{\pi}{2}-0.sin0+cost|^{\dfrac{\pi}{2}}_0\right]=2\left[\dfrac{\pi}{2}-0-1\right]=\pi-2\)

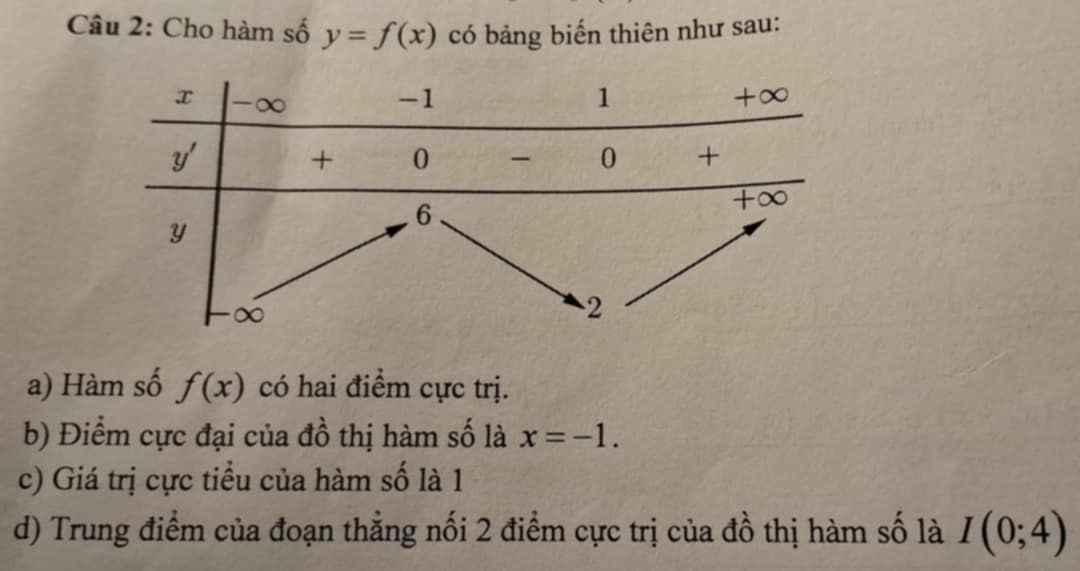
a) Theo BBT ta thấy \(f\left(x\right)\) đạt cực trị tại 2 điiểm có hoành độ \(x=-1;x=1\)

\(\Rightarrow\) Chọn Đúng

b) Điểm cực đại \(x=-1;y=6\)

\(\Rightarrow\) Chọn Đúng

c) Giá trị cực tiểu của hàm số là \(2\) tại \(x=1\)

\(\Rightarrow\) Chọn Sai

d) Tọa độ 2 điểm cực trị là \(A\left(-1;6\right);B\left(1;2\right)\)

\(I\) là trung điểm \(AB\Rightarrow I\left(\dfrac{-1+1}{2};\dfrac{6+2}{2}\right)=\left(0;4\right)\)

\(\Rightarrow\) Chọn Đúng

a) Đặt hệ trục tọa độ \(Oxyz:\)

\(A\left(0;0;0\right);B\left(a;0;0\right);C\left(a;a\sqrt{3};0\right);D\left(0;a\sqrt{3};0\right);S\left(0;0;a\right)\)

\(\overrightarrow{SB}=\left(a;0;-a\right);\overrightarrow{SD}=\left(0;a\sqrt{3};-a\right)\)

\(\Rightarrow\overrightarrow{n\left(SBD\right)}=\left[\overrightarrow{SB}.\overrightarrow{SD}\right]=\left(a^2\sqrt{3};a^2;a^2\sqrt{3}\right)=\left(\sqrt{3};1;\sqrt{3}\right)\)

\(\Rightarrow\left(SBD\right):\sqrt{3}\left(x-a\right)+\left(y-0\right)+\sqrt{3}\left(z-0\right)=0\)

\(\Rightarrow\left(SBD\right):\sqrt{3}x+y+\sqrt{3}z-a\sqrt{3}=0\)

\(d\left(C;\left(SBD\right)\right)=\dfrac{\left|\sqrt{3}.a+a\sqrt{3}+\sqrt{3}.0-a\sqrt{3}\right|}{\sqrt{3+1+3}}=\dfrac{a\sqrt{21}}{7}\)

b) \(\overrightarrow{SC}=\left(a;a\sqrt{3};-a\right);\overrightarrow{SD}=\left(0;a\sqrt{3};-a\right)\)

\(\Rightarrow\overrightarrow{n\left(SCD\right)}=\left[\overrightarrow{SC}.\overrightarrow{SD}\right]=\left(a^2\sqrt{3};a^2;0\right)=\left(\sqrt{3};1;0\right)\)

\(\Rightarrow\left(SCD\right):\sqrt{3}\left(x-0\right)+\left(y-0\right)+0\left(z-a\right)=0\)

\(\Rightarrow\left(SCD\right):\sqrt{3}x+y=0\)

\(G\) là trọng tâm \(\Delta SBD\Rightarrow G\left(\dfrac{0+0+a}{3};\dfrac{0+0+a\sqrt{3}}{3};\dfrac{a+0+0}{3}\right)=\left(\dfrac{a}{3};\dfrac{a\sqrt{3}}{3};\dfrac{a}{3}\right)\)

\(d\left(G;\left(SCD\right)\right)=\dfrac{\left|\sqrt{3}.\dfrac{a}{3}+\dfrac{a\sqrt{3}}{3}\right|}{\sqrt{3+1}}=\dfrac{a\sqrt{3}}{3}\)