Chuyên đề thể tích 1

Để tính thể tích SAPMQ, ta cần tìm độ dài đoạn PM và đoạn MQ. Gọi E là trung điểm của BD. Ta có ME song song với AM và ME = 1/2 BD = 1/2 a. Vì (∆) song song với BD nên góc AME = góc ABD = 45 độ. Vì SA vuông góc với ABCD nên góc SAM = 90 độ. Vì SA = a√3 và góc SAM = 90 độ nên tam giác SAM là tam giác vuông cân tại A. Do đó, góc ASM = 45 độ. Vì góc ASM = góc AME = 45 độ nên tam giác ASM và tam giác AME đồng dạng. Vậy, ta có: AM/AS = AE/AM AM^2 = AS * AE AM^2 = (a√3) * (1/2 a) AM^2 = a^2 * √3 / 2 AM = a√3 / √2 AM = a√6 / 2 Ta có ME = 1/2 a Vậy, PM = AM - ME = (a√6 / 2) - (1/2 a) = (a√6 - a) / 2 Tương tự, ta có MQ = AM + ME = (a√6 / 2) + (1/2 a) = (a√6 + a) / 2 Vậy, thể tích SAPMQ = SABC * PM = a^2 * (a√6 - a) / 2 = a^3√6 / 2 - a^3 / 2

Ủa rồi đoạn đề bài yêu cầu tính đâu nhỉ? Ko thấy yêu cầu làm gì cả?

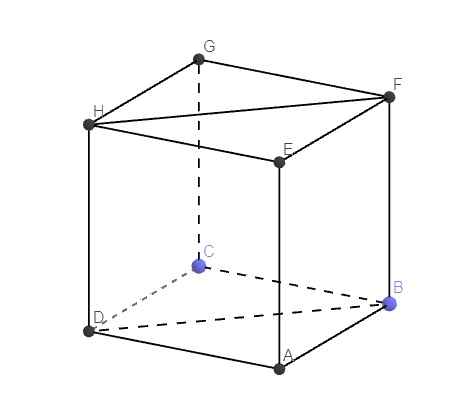
Điều duy nhất cần để ý là đọc thật kĩ đề, mặt cắt ở đây là mặt cắt chéo chứ không phải mặt cắt thẳng góc của khối lập phương.

Có nghĩa nó là thiết diện dạng BDHF như hình dưới chứ ko phải thiết diện ngang như ABCD hay ABFE đâu

Gọi cạnh lập phương là 1 đơn vị \(\Rightarrow V_{ }\) lập phương bằng 1

\(4R=BH\) với \(BH=\sqrt{AB^2+AD^2+DH^2}=\sqrt{3}\Rightarrow R=\dfrac{\sqrt{3}}{4}\)

\(\Rightarrow V_{1-Cr}=\dfrac{4}{3}\pi R^3=\dfrac{\pi\sqrt{3}}{16}\)

\(\Rightarrow V_{Cr}=\left(1+8.\dfrac{1}{8}\right)V_{1-Cr}=\dfrac{\pi\sqrt{3}}{8}\)

\(\%\) ô trống \(=\left(1-\dfrac{\pi\sqrt{3}}{8}\right).100\%=32\%\)

\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)

Kẻ \(AE\perp SB\Rightarrow AE\perp\left(SBC\right)\Rightarrow AE\perp SC\)

Kẻ \(AD\perp SC\Rightarrow SC\perp\left(ADE\right)\)

\(\Rightarrow\widehat{ADE}\) là góc giữa (SAC) và (SBC)

\(\Rightarrow\widehat{ADE}=60^0\)

\(\Rightarrow AE=AD.sin\widehat{ADE}=AD.sin60^0=\dfrac{AD\sqrt{3}}{2}\Rightarrow\dfrac{1}{AE^2}=\dfrac{4}{3AD^2}\)

Áp dụng hệ thức lượng:

\(\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\) ; \(\dfrac{1}{AD^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\)

\(\Rightarrow\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{4}{3}\left(\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\right)\)

\(\Rightarrow\dfrac{1}{AB^2}=\dfrac{4}{3}.\dfrac{1}{AC^2}+\dfrac{1}{3SA^2}=\dfrac{4}{3}.\dfrac{1}{AB^2+16a^2}+\dfrac{1}{27a^2}\)

Đề có nhầm lẫn đâu không nhỉ, vì phương trình \(\dfrac{1}{x}=\dfrac{4}{3\left(x+16\right)}+\dfrac{1}{27}\) cho nghiệm  rất xấu

Lời giải:
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp  (ABCD)$

Vì $SA\perp (ABCD)$ nên $SA\perp CB$

Mà: $AB\perp CB$

$\Rightarrow CB\perp (SAB)$

$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$

$\Rightarrow SB=CB=a$

$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)