cho x, y, z là nghiệm bất phương trình \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\xy+yz+zx=4\end{matrix}\right.\)
Chứng minh rằng \(-\dfrac{8}{3}\) ≤ x, y, z ≤ \(\dfrac{8}{3}\)
cho x, y, z là nghiệm bất phương trình \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\xy+yz+zx=4\end{matrix}\right.\)
Chứng minh rằng \(-\dfrac{8}{3}\) ≤ x, y, z ≤ \(\dfrac{8}{3}\)
Cho b > c > d Chứng minh rằng : ( a + b + c )2 > 8( ac + bd ) với mọi a
Với $a=1; b=5; c=4; d=3$ thì BĐT sai. Bạn xem lại đề.
cho a2 + b2 ≤ 1. Chứng minh rằng ( ac + bd - 1 )2 ≥ ( a2 + b2 - 1 )(c2 + d2 -1 )
Nếu \(c^2+d^2\ge1\left(bất.đẳng.thức.đúng\right)\)
Ta chứng minh c2+d2<1
+Đặt x=1-a2-b2 và y =1-c2 - d2
-0 \(\le x,y\le1\)
Bđt <=> (2 - 2ac - 2bd)2\(\ge\) 4xy <=> ((a-c)2+(b-d)2+x+y)2\(\ge4xy\)
=> ((a-c)2+(b-d)2 + x + y)2 \(\ge\left(x+y\right)^2\ge4xy\left(đpcm\right)\)
Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình m2(x4 - 1) + m(x2 - 1) - 6(x - 1) ≥ 0 đúng với mọi x ∈ R. Tổng giá trị của tất cả các phần tử thuộc S bằng bao nhiêu ?
Lời giải:
$f(x)=m^2(x^4-1)+m(x^2-1)-6(x-1)=(x-1)[m^2(x+1)(x^2+1)+m(x+1)-6]$
Để $f(x)\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$m^2(x+1)(x^2+1)+m(x+1)-6=Q(x)(x-1)^k$ với $k$ là số lẻ
$\Rightarrow h(x)=m^2(x+1)(x^2+1)+m(x+1)-6\vdots x-1$
$\Rightarrow h(1)=0$
$\Leftrightarrow 4m^2+2m-6=0$
$\Leftrightarrow 2m^2+m-3=0$
$\Leftrightarrow (m-1)(2m+3)=0\Rightarrow m=1$ hoặc $m=\frac{-3}{2}$
Thay các giá trị trên vào $f(x)$ ban đầu thì $m\in \left\{1; \frac{-3}{2}\right\}$
Tổng các giá trị của các phần tử thuộc $S$: $1+\frac{-3}{2}=\frac{-1}{2}$
Tìm m để : 3x2 + 6x + m ≥ 0 với mọi x ϵ [0;+∞)
Δ=6^2-4*3*m=36-12m
Để BPT luôn đúng khi x>=0 thì 36-12m<0
=>12m>36
=>m>3
Điều kiện để \(ax+by>c\) là 1 bất phương trình bậc nhất 2 ẩn x, y là:
A. \(a\ne0\). B. \(b\ne0\). C. \(a^2+b^2\ge0\). D. \(a^2+b^2\ne0\).
Giải bất phương trình: \(\sqrt{x^2-4x}>x-3\)
\(\sqrt{x^2-4x}>x-3\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-3< 0\\x^2-4x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-3\ge0\\x^2-4x>\left(x-3\right)^2\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 3\\\left[{}\begin{matrix}x\le0\\x\ge4\end{matrix}\right.\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge3\\x>\dfrac{9}{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le0\\x>\dfrac{9}{2}\end{matrix}\right.\)
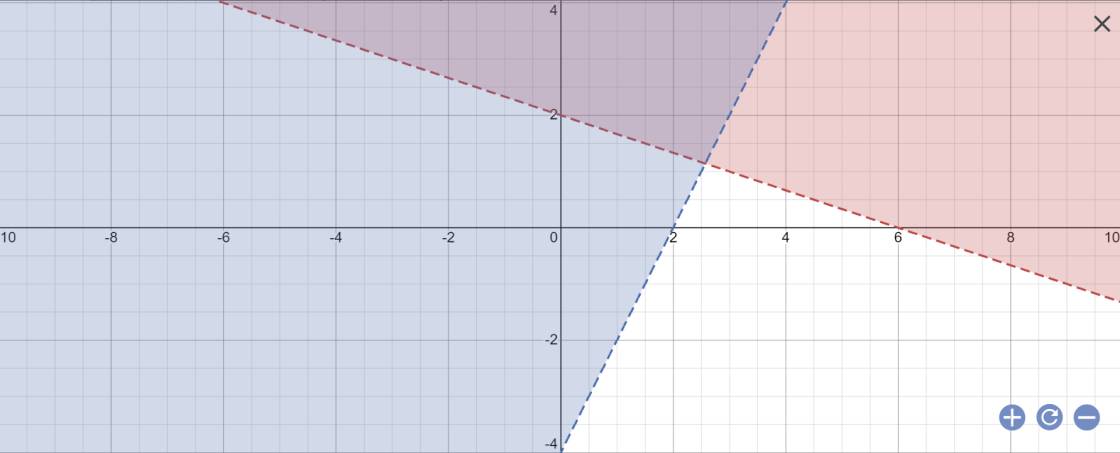
Biểu diễn miền nghiệm hệ bất phương trình \(\left\{{}\begin{matrix}2\left(x+y\right)+1>x-y+7\\2x-y< 4\end{matrix}\right.\).
=>2x+2y+1>x-y+7 và 2x-y<4
=>x+3y>6 và 2x-y<4