=>2x+2y+1>x-y+7 và 2x-y<4
=>x+3y>6 và 2x-y<4
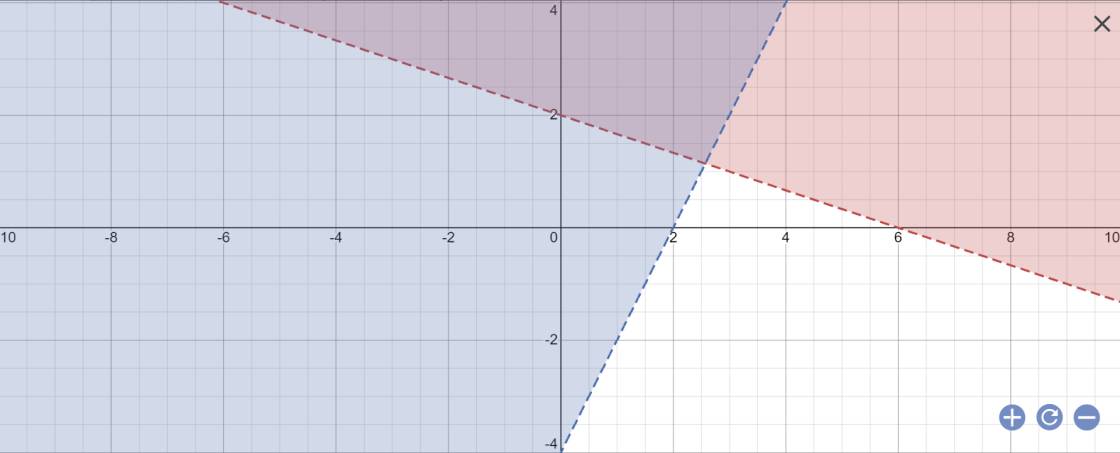
=>2x+2y+1>x-y+7 và 2x-y<4
=>x+3y>6 và 2x-y<4

Tìm m để hệ bất phương trình có nghiệm duy nhất
a) \(\left\{{}\begin{matrix}2x-1\ge3\\x-m\le0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}m^2x\ge6-x\\3x-1\le x+5\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge x^2+7x+1\\2m\le8+5x\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}mx\le m-3\\\left(m+3\right)x\ge m-9\end{matrix}\right.\)
e)\(\left\{{}\begin{matrix}2m\left(x+1\right)\ge x+3\\4mx+3\ge4x\end{matrix}\right.\)
Tìm m để hệ bất phương trình vô nghiệm
a) \(\left\{{}\begin{matrix}3x+4>x+9\\1-2x\le m-3x+1\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}2x+7\ge8x+1\\m+5< 2x\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge x^2+7x+1\\2m\le8+5x\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}3x+5\ge x-1\\\left(x+2\right)^2\le\left(x-1\right)^2+9\\mx+1>\left(m-2\right)x+m\end{matrix}\right.\)
e) \(\left\{{}\begin{matrix}2\left(x-3\right)< 5\left(x-4\right)\\mx+1\le x-1\end{matrix}\right.\)
1tìm m để hệ bất phương trình có nghiệm duy nhất \(\left\{{}\begin{matrix}2x-1\ge3\\x-m\le0\end{matrix}\right.\)
2hệ bất phương trình \(\left\{{}\begin{matrix}2x-1>0\\x-m< 2\end{matrix}\right.\)có nghiệm khi ??
3 hệ bất phương trình có nghiệm khi \(\left\{{}\begin{matrix}x+m\le0\\x^2-x+4< x^2-1\end{matrix}\right.\)
4 tìm tất cả các giá trị của m đề với mọi giá trị của x thỏa mãn \(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\)
5 với giá trị nào của m thì hệ có nghiệm \(\left\{{}\begin{matrix}x^2+y^2=1\\x+y\sqrt{3}< m\end{matrix}\right.\)
6 với giá trị nào của m thì hệ có nghiệm duy nhất \(\left\{{}\begin{matrix}x^2+2x+a\le0\\x^2-4x-6a\le0\end{matrix}\right.\)
Tìm m để hệ bất phương trình có nghiệm
a) \(\left\{{}\begin{matrix}2x-1>0\\x-m< 2\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}3\left(x-6\right)< -3\\\dfrac{5x+m}{2}>7\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}x^2-1\le0\\x-m>0\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}x-2\ge0\\\left(m^2+1\right)x< 4\end{matrix}\right.\)
e) \(\left\{{}\begin{matrix}m\left(mx-1\right)< 2\\m\left(mx-2\right)\ge2m+1\end{matrix}\right.\)
tìm m để hệ bất phương trình \(\left\{{}\begin{matrix}\left(3-x\right)\left(4-x\right)lớnhơn0\\x< m-1\end{matrix}\right.\) vô nghiệm
Tìm m để hệ bất phương trình có nghiệm \(\left\{{}\begin{matrix}-x^2+2x+3\le0\\x+2m-1>0\end{matrix}\right.\)
Tìm m để hệ bất phương trình có nghiệm \(\left\{{}\begin{matrix}-x^2+2x+3\le0\\x+2m-1>0\end{matrix}\right.\)
Tìm Min của biểu thức F=y-x trên miền xác định bởi hệ \(\left\{{}\begin{matrix}2x+y\le2\\x-y\le2\\5x+y\ge-4\end{matrix}\right.\)
Cho các số x,y ϵ R thỏa mãn hệ bất phương trình sau \(\left\{{}\begin{matrix}x+y\ge3\\x\ge0\\y\ge0\\2x+y\le6\end{matrix}\right.\). Tìm giá trị nhỏ nhất và lớn nhất của biểu thức: F = 5x-6y+2021
giải hệ phương trình
a) \(\left\{{}\begin{matrix}\sqrt{2x^2+2y^2}+\sqrt{\frac{4}{3}\left(x^2+xy+y^2\right)}=2\left(x+y\right)\\\sqrt{3x+1}+\sqrt{5x+4}=3xy-y+3\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}\sqrt{5x^2+2xy+2y^2}+\sqrt{2x^2+2xy+5y^2}=3\left(x+y\right)\\\sqrt{x+2y+1}+2\sqrt[3]{12x+7y+8}=2xy+x+5\end{matrix}\right.\)
c)\(\left\{{}\begin{matrix}x^2+xy+x+3=0\\\left(x+1\right)^2+3\left(y+1\right)+2\left(xy-\sqrt{x^2y+2y}\right)=0\end{matrix}\right.\)