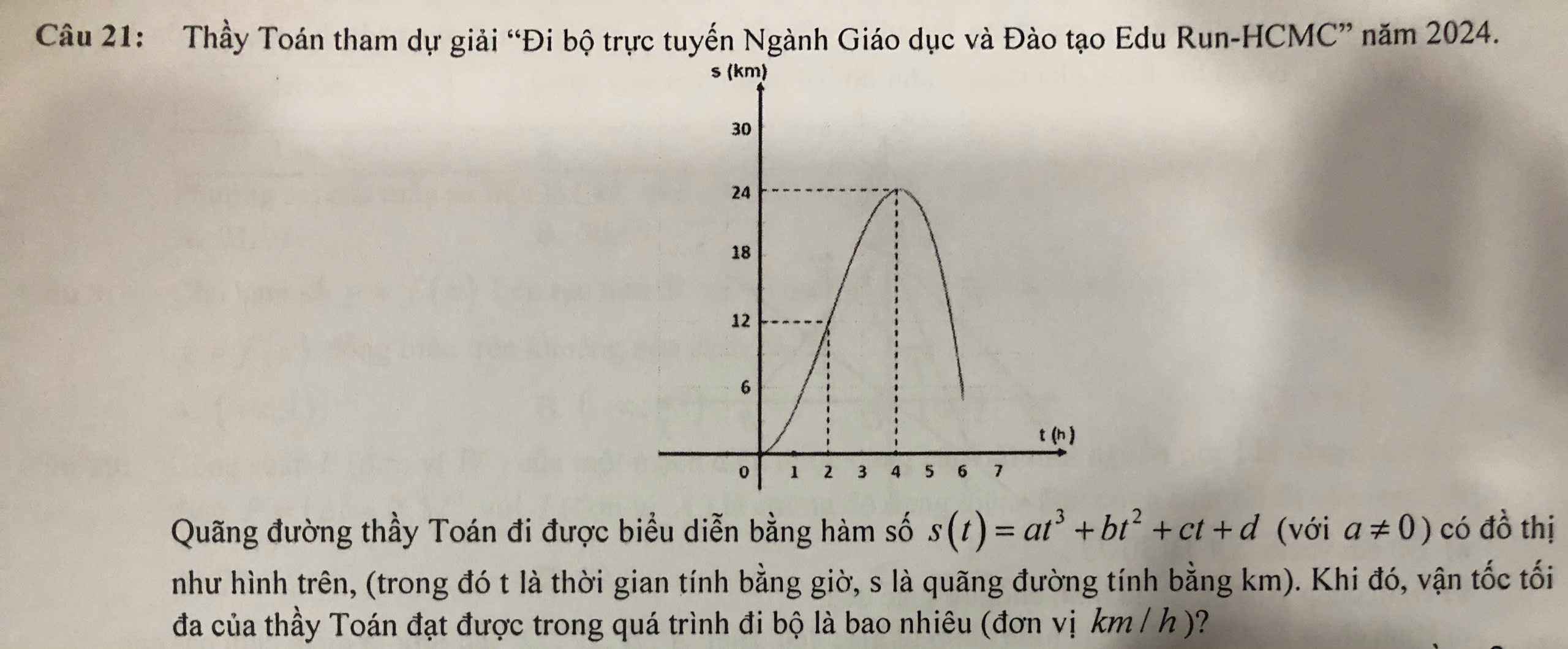
Bài tập cuối chương I

Để hàm số có 1 cực tiểu

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{4}>0\\-2m\ge0\end{matrix}\right.\Rightarrow m\le0}\)

Chọn đáp án D

Để hàm số có 1 cực tiểu

Chọn đáp án D

\(y'=x^3-4mx=x\left(x^2-4m\right)\)

\(y'=0\Leftrightarrow x\left(x^2-4m\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=4m\end{matrix}\right.\)

Hàm số có 1 cực tiểu khi và chỉ khi

\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{4}>0\left(đúng\right)\\-2m\ge0\end{matrix}\right.\)

\(\Leftrightarrow m\le0\)

Nên chọn D

\(y=\dfrac{2\left(x+1\right)}{x^2-2mx+4}\)

\(\lim\limits_{x\rightarrow\infty}y=0\) \(\Rightarrow\) Hàm số có \(TCN:y=0\)

Để Hàm số có 3 tiệm cận khi \(x^2-2mx+4=0\) có 2 nghiệm phân biệt \(x\ne-1\)

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-4>0\\\left(-1\right)^2-2m.\left(-1\right)+4\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m^2>4\\2m\ne-5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\cup m>2\\m\ne-\dfrac{5}{2}\end{matrix}\right.\)

\(\Leftrightarrow m< -\dfrac{5}{2}\cup-\dfrac{5}{2}< m< -2\cup m>2\)

\(\Leftrightarrow m\in\left(-\infty;-\dfrac{5}{2}\right)\cup\left(-\dfrac{5}{2};-2\right)\cup\left(2;+\infty\right)\)

Vậy chọn A

\(f'\left(x\right)=0\Rightarrow x=0;82\)

\(u=x^4-18x^2+m\)

\(u'=4x^3-36x=0\Rightarrow x=\left\{-3;0;3\right\}\)

BBT hàm u:

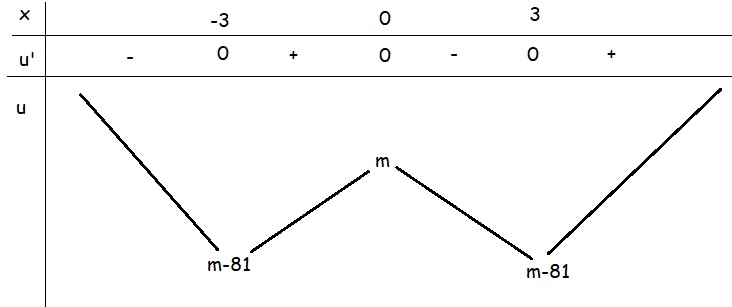
Do u có 3 cực trị nên hàm có đúng 7 cực trị khi 2 đường thẳng \(y=0\) và \(y=82\) cắt \(u\left(x\right)\) tại tổng cộng 4 điểm nghiệm đơn

TH1: \(y=0\) ko cắt (hoặc chỉ tiếp xúc) u(x), còn \(y=82\) cắt u(x) tại 4 điểm pb

 \(\Rightarrow\left\{{}\begin{matrix}m-81\ge0\\m-81< 82< m\end{matrix}\right.\)  \(\Leftrightarrow82< m< 163\)

Có 80 m nguyên dương

TH2: y=0 và y=82 đều cắt u(x) tại 2 điểm pb

\(\Rightarrow\left\{{}\begin{matrix}m\le0\\m\le82\end{matrix}\right.\) \(\Rightarrow m\le0\) (ko có m nguyên dương)

C đúng

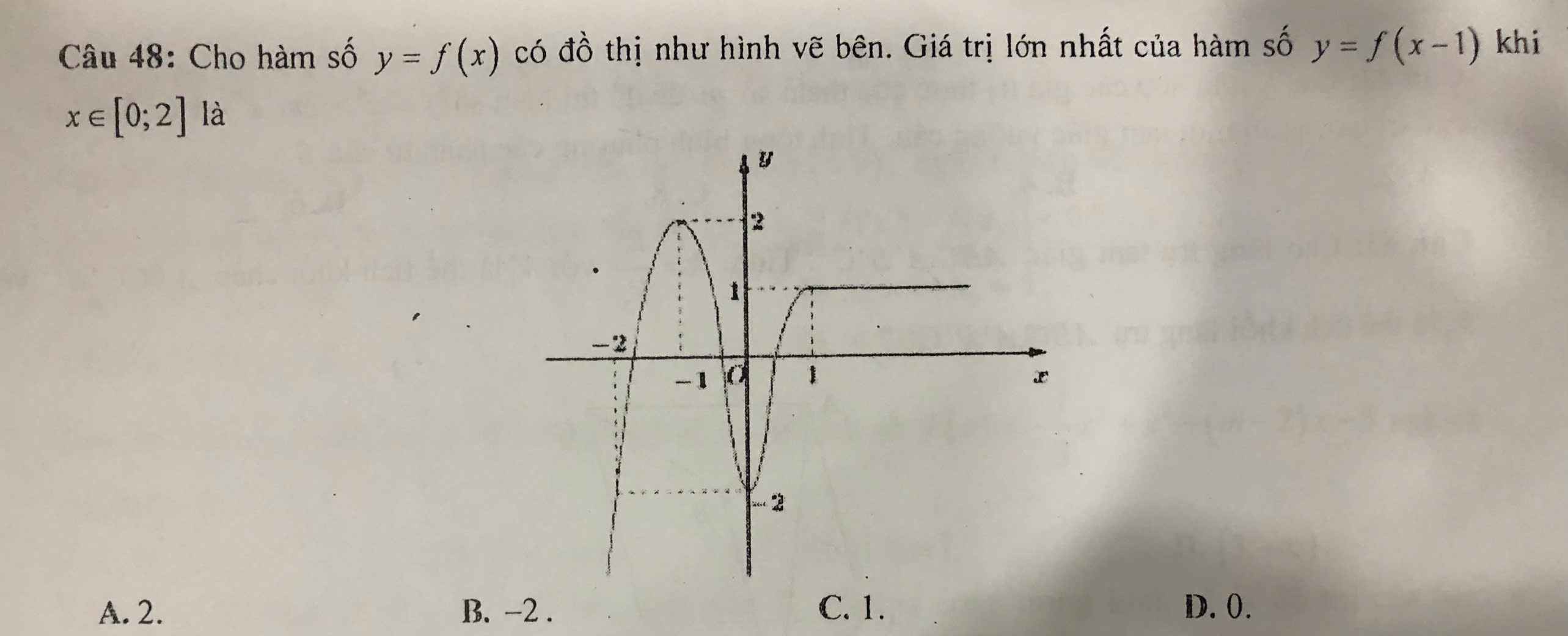
Đồ thị hàm số y=f(x-1) là đồ thị hàm số y=f(x) tịnh tiến sang bên phải 1 đơn vị nên có dạng như hình sau

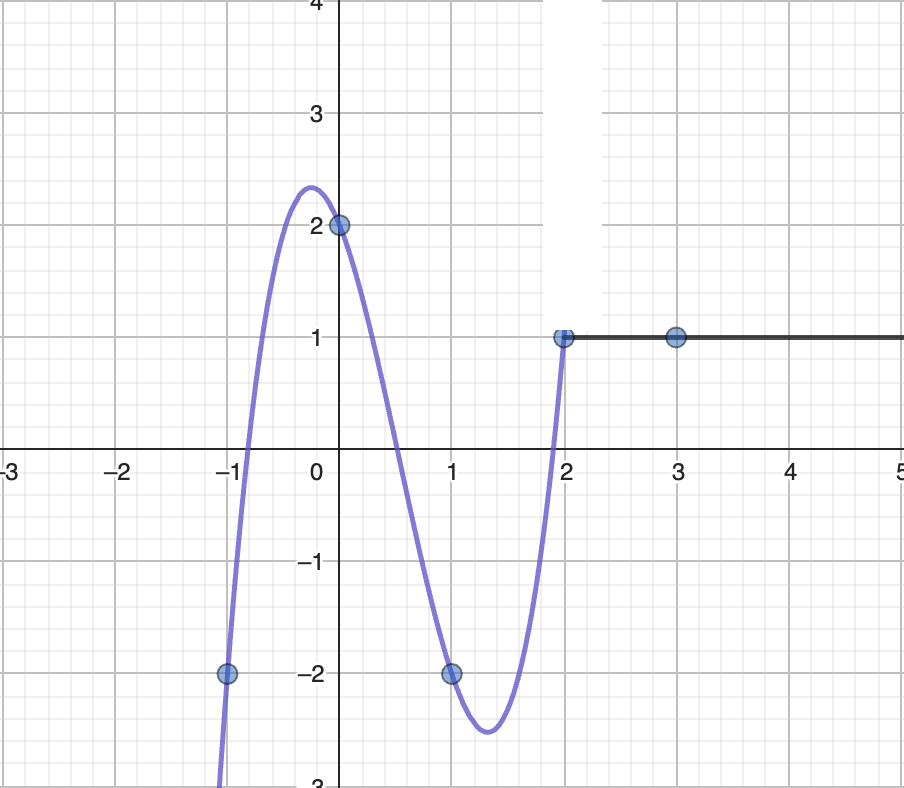
Từ đồ thị ta thấy GTLN của hàm số y=f(x-1) khi x \(\in\) [0;2] là 2 tại x=0.

Chọn đáp án A.

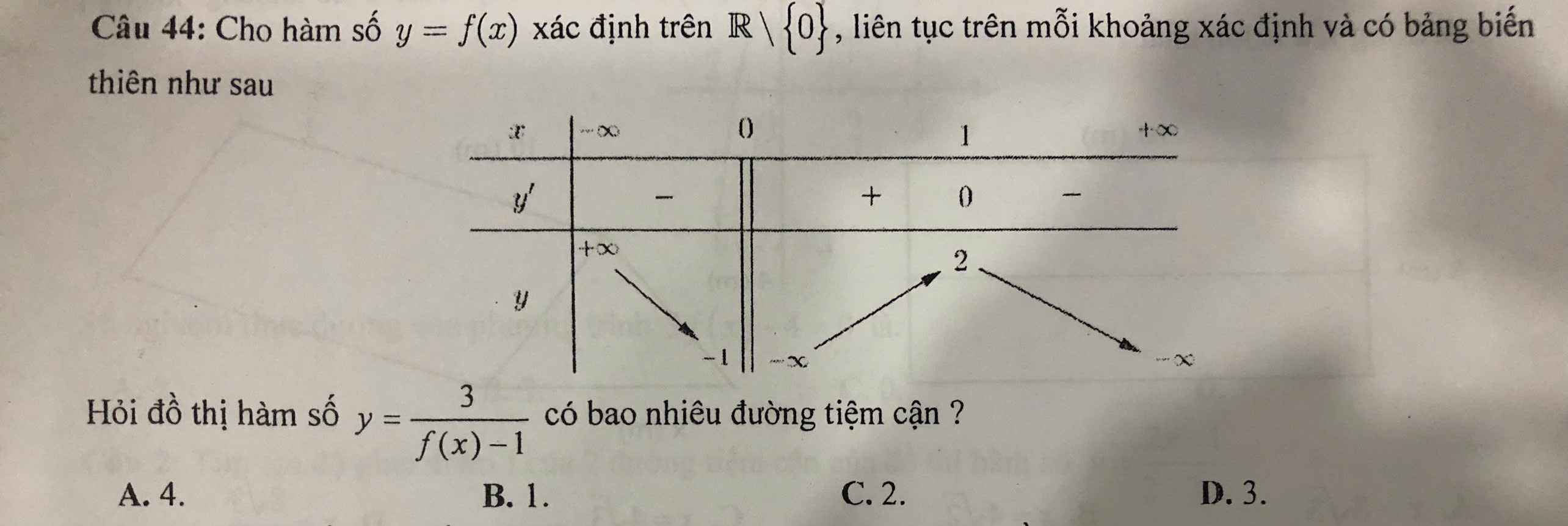
Dựa vào BBT ta thấy \(y=f\left(x\right)\) có 2 tiệm cận là \(TCĐ:x=0;TCN:y=-1\)

\(\Rightarrow f\left(x\right)-1\) có 2 tiệm cận \(x=0;y=-2\)

Nên \(f\left(x\right)\) là hàm phân thức cùng bậc ví dụ \(y=\dfrac{-2x+a}{x}\)

\(\Rightarrow y=\dfrac{3}{f\left(x\right)-1}\) cũng có 2 tiệm cận (TCĐ sẽ là \(x=\dfrac{a}{2}\) còn TCN  là \(y=-\dfrac{3}{2}\))

Vậy chọn C

\(\lim\limits_{x\rightarrow\pm\infty}f\left(x\right)=\infty\) nên \(\lim\limits_{x\rightarrow\infty}\dfrac{3}{f\left(x\right)-1}=0\)

Do đó \(y=0\) là 1 TCN

Từ đồ thị ta thấy đường thẳng \(y=1\) cắt \(y=f\left(x\right)\) tại 3 điểm phân biệt

\(\Rightarrow f\left(x\right)-1=0\) có 3 nghiệm pb

\(\Rightarrow y=\dfrac{3}{f\left(x\right)-1}\) có 3 TCĐ

Vậy ĐTHS có tổng cộng 4 tiệm cận

\(y'=4x^3+4mx=4x\left(x^2+m\right)\)

Để đồ thị hàm số chỉ có một điểm cực trị thì \(y'=0\) phải có duy nhất \(\) một nghiệm đơn \(x=0\) hoặc nghiệm kép \(x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}-4m< 0\\-4m=0\end{matrix}\right.\) \(\Leftrightarrow m\ge0\left(1\right)\)

Khô đó điểm cực trị có tọa độ \(x=0\Rightarrow y=-m^2+3m\) hay \(\left(0;-m^2+3m\right)\)

\(y=-4\Leftrightarrow-m^2+3m=-4\)

\(\Leftrightarrow m^2-3m-4=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m=-1\left(không.thỏa\left(1\right)\right)\\m=4\end{matrix}\right.\)

\(\Leftrightarrow m=4\)

Vậy chọn C

\(y'=3x^2-\dfrac{27}{x^2}\)

\(y'=0\Leftrightarrow3x^2-\dfrac{27}{x^2}=0\)

\(\Leftrightarrow3x^4=27\left(x\ne0\right)\)

\(\Leftrightarrow x=\pm3\)

\(\Rightarrow x=3\) \(\left(x\in\left(0;+\infty\right)\right)\)

Lập bảng biến thiên ra thấy hàn số đạt cực tiểu tại \(x=3\)

\(y\left(3\right)=3^3+\dfrac{27}{3}-8=18>4\)

Vậy chọn D

\(y=x^3+\dfrac{9}{x}+\dfrac{9}{x}+\dfrac{9}{x}-18\ge4\sqrt[4]{\dfrac{729x^3}{x^3}}-18=12\sqrt{3}-18\in\left(2;3\right)\)

B là đáp án đúng

Sửa lại \(x=\pm\sqrt{3}\Rightarrow x=\sqrt{3}\)

\(m=y\left(\sqrt{3}\right)=3\sqrt{3}+9\sqrt{3}-18=12\sqrt{3}-18\)

\(\Rightarrow0< m< 2\)

Chọn B

Đặt \(\dfrac{x}{2}=t\)

\(x\in\left[0;2\right]\Rightarrow t\in\left[0;1\right]\)

Từ đồ thị ta thấy hàm \(y=f\left(t\right)\) trên \(\left[0;1\right]\) có \(y_{max}=y\left(0\right)=2\) và \(y_{min}=y\left(1\right)=0\)

\(\Rightarrow y=\dfrac{3}{2}f\left(\dfrac{x}{2}\right)=\dfrac{3}{2}f\left(t\right)\) có \(M=\dfrac{3}{2}.2=3\) và \(m=\dfrac{3}{2}.0=0\)

\(\Rightarrow M+m=3\)