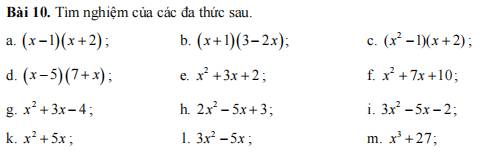Bài 9: Nghiệm của đa thức một biến

\(\dfrac{5}{7}x^3.\dfrac{2}{3}x^4.\left(-\dfrac{7}{10}x\right)\)

\(=\dfrac{5}{7}.\dfrac{2}{3}.\left(-\dfrac{7}{10}\right).\left(x^3.x^4.x\right)\)

\(=-\dfrac{1}{3}x^8\)

+ Phần hệ số: \(-\dfrac{1}{3}\)

+ Phần biến: \(x^8\)

M(x)=x^2-6x+15

=x^2-6x+9+6

=(x-3)^2+6>=6>0 với mọi x

=>M(x) ko có nghiệm

a/\(3x-15=0\)
\(\Rightarrow3x=15\)
\(\Rightarrow x=5\)
Vậy nghiệm của A là x = 5
b/\(\left(x-2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Vậy nghiệm của B là \(x\in\left\{2;-3\right\}\)
c/\(\left(2x-1\right)\left(x^2+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-1=0\\x^2+2=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=1\\x^2=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\dfrac{1}{2}\)
Vậy nghiệm của C là \(x=\dfrac{1}{2}\)
d/\(3x^2-6x=0\)
\(\Rightarrow x\left(3x-6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\3x-6=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\3x=6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy nghiệm của D là \(x\in\left\{0;2\right\}\)

e/\(2x\left(x-3\right)-5\left(x-3\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-5=0\\x-3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2x=5\\x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=3\end{matrix}\right.\)
Vậy nghiệm của E là \(x\in\left\{\dfrac{5}{2};3\right\}\)

Lời giải:
Ta thấy:

$3x^2-4x+12=x^2+(2x^2-4x+2)+10=x^2+2(x^2-2x+1)+10$

$=x^2+2(x-1)^2+10\geq 10>0$ với mọi $x$

Do đó đa thức $3x^2-4x+12$ vô nghiệm.

Đặt 2x^3-2x+3-19=0

=>2x^3-2x-16=0

=>x^3-x-8=0

=>\(x\simeq2,17\)

\(P\left(x\right)=x^3-x^2-4x+4=0\\ \Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)=0\\ \Leftrightarrow\left(x^2-4\right).\left(x-1\right)=0\\ \Leftrightarrow\left(x-2\right).\left(x+2\right).\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=1\end{matrix}\right.\)

Chọn B

R(x)=0

=>x(x^2-2)=0

=>x=0 hoặc \(x=\pm\sqrt{2}\)

S(x)=0

=>x^2+1=0(vô lý)

giúp tôi vs  tôi  cần gấp 

a: P(x)=2x^3-x^2+3x+20

Q(x)=-x^3-x^2-3x-4

b: K(x)=2x^3-x^2+3x+20-x^3-x^2-3x-4

=x^3-2x^2+16

H(x)=2x^3-x^2+3x+20+x^3+x^2+3x+4

=3x^3+6x+24

c: K(-2)=(-2)^3-2*(-2)^2+16=0

=>x=-2 là nghiệm của K(x)

H(-2)=3*(-2)^3+6*(-2)+24=24-12-3*8=-12<>0

=>x=-2 ko là nghiệm

a/\(16x-81x^5=0\)
\(\Rightarrow x\left(16-81x^4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\16-81x^4=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\81x^4=16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^4=\dfrac{16}{81}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
Vậy nghiệm của đa thức là \(x\in\left\{0;\dfrac{2}{3}\right\}\)
b/\(x^2-7x=0\)
\(\Rightarrow x\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-7=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)
Vậy nghiệm của đa thức là \(x\in\left\{0;7\right\}\)

a: (x-1)(x+2)=0

=>x-1=0 hoặc x+2=0

=>x=1 hoặc x=-2

b: (x+1)(3-2x)=0

=>x+1=0 hoặc 3-2x=0

=>x=3/2 hoặc x=-1

c: (x^2-1)(x+2)=0

=>x+2=0 hoặc x^2-1=0

=>\(x\in\left\{1;-1;-2\right\}\)

d: (x-5)(x+7)=0

=>x-5=0 hoặc x+7=0

=>x=5 hoặc x=-7

e: x^2+3x+2=0

=>(x+1)(x+2)=0

=>x=-1 hoặc x=-2

f: x^2+7x+10=0

=>(x+2)(x+5)=0

=>x=-2 hoặc x=-5

g: x^2+3x-4=0

=>(x+4)(x-1)=0

=>x=1 hoặc x=-4