Cho tam giác ABC vuông tại A
AB=5cm; AC=3cm
I là trung điểm AB. D là điểm đối xứng C qua I
a, ADBC là hình gì ?
b, K là trung điểm BC. Chứng minh rằng: IK//AC
c, Diện tích của tam giác ABC
Cho tam giác ABC vuông tại A
AB=5cm; AC=3cm
I là trung điểm AB. D là điểm đối xứng C qua I
a, ADBC là hình gì ?
b, K là trung điểm BC. Chứng minh rằng: IK//AC
c, Diện tích của tam giác ABC
a: Xét tứ giác ADBC có
I là trung điểm chung của AB và DC
nên ADBC là hình bình hành
b: Xét ΔBAC có BI/BA=BK/BC
nên IK//AC
c: \(S_{ABC}=\dfrac{1}{2}\cdot3\cdot5=1.5\cdot5=7.5\left(cm^2\right)\)
Cho đường thẳng a và b song song với nhau. A và B là hai điểm cố định trên đường thẳng a. Còn C là điểm di động trên đường thẳng b. Chứng tỏ rằng diện tích tam giác ABC không thay đổi khi C chạy trên b
Cho ∆ABC vuông tại A, có AB = 8cm, BC bằng 10cm. Diện tích ABC bằng?
Áp dụng Pytago vào tam giác \(ABC\)
\(AB^2+AC^2=BC^2\\ =>AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-8^2}=6\left(cm\right)\)
Diện tích tam giác
\(S=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.8.6=24\left(cm^2\right)\)
Cho tam giác ABC cân tại A vẽ D đối xứng C qua A tính diện tích tam giác BCD biết BA=5 và BC=6
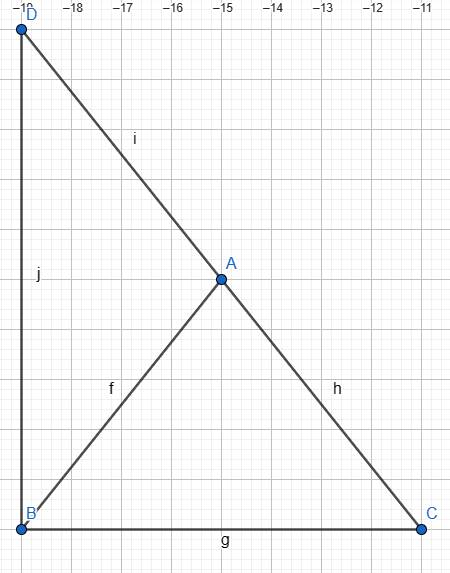
Sorri lỡ vẽ hình bự quá :D
\(\Delta ABC\) cân tại A => AB = AC (1)
D đối xứng với C qua A => A là trung điểm CD => AC = AD => AC=\(\dfrac{CD}{2}\)(2)
Từ (1) và (2) => \(AB=\dfrac{CD}{2}\)
Xét \(\Delta BCD\) có A là tđ CD => AB là trung tuyến
Mà \(AB=\dfrac{CD}{2}\) nên \(\Delta BCD\) vuông tại B
Độ dài cạnh CD: CD = 2.AB = 2.5 = 10 (cm)
Bây giờ áp dụng định lý Pytago để tính BD
Áp dụng đlý Pytago vào \(\Delta BCD\) vuông tại B ta có:
\(BC^2+BD^2=CD^2\\ =>6^2+BD^2=10^2\\ =>36+BD^2=100\\ =>BD^2=100-36=64\\ =>BD=\sqrt{64}=8\left(cm\right)\)
Diện tích \(\Delta BCD\): \(\dfrac{BD.BC}{2}=\dfrac{8.6}{2}=\dfrac{48}{2}=24\left(cm^2\right)\)
Vì đề k cho đơn vị nên mình để cm nha ![]()
Cho tam giác ABC cân tại A vẽ D đối xứng C qua A tính diện tích tam giác ABC biết BA=5 và BC=6
dễ dàng chứng minh được BCD là tam giác vuông tại B
từ đó tính được BD
Có : SBCD = 1/2.BD.BC= 1/2.8.6 = 24
có : BA là đường trung tuyến của △BCD.
=> SABC = 1/2. SBCD =1/2. 24 = 12
Cho tam giác ABC góc A=90 độ.Gọi E F G là trung điểm của AB,BC,AC
a) tứ giác AEGF là hình gì?
b) AB=6cm,AC=8cm.Tính độ dài AG
a: Xét ΔCAB có CF/CA=CG/CB
nên FG//AB và FG=AB/2
=>FG//AE và FG=AE
=>AEGF là hình bình hành
mà góc FAE=90 độ
nên AEGF là hình chữ nhật
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AG=BC/2=5cm
1 Cho tam giác ABC ; AB = AC = 10 cm ; BC =12 cm
Tính diện tích ABC và đg cao BK vẽ hình cho tui nhóe =))
2 Cho tam giác ABC có S = 60 cm vuông , lấy M là TĐ BC , N thuộc AC sao cho AN = 1 phần 3 AC . Tính diện tích ABM và ABN vẽ hình cho tui nhóe =))
Thank các bro
Câu 1:
\(P=\dfrac{10+10+12}{2}=\dfrac{32}{2}=16\left(cm\right)\)
\(S=\sqrt{16\cdot\left(16-12\right)\cdot\left(16-10\right)\cdot\left(16-10\right)}=\sqrt{16\cdot4\cdot6\cdot6}=6\cdot2\cdot4=48\left(cm^2\right)\)
\(BK=48\cdot2:10=9,6\left(cm\right)\)
Các bạn giúp mình bài 3 với nhé.Mình đang cần gấp😘😘😘
Bài 3:
a: Xét ΔABC có AE/AB=AF/AC
nên EF//BC và EF=1/2BC=7,5cm
\(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
S=1/2*9*12=54cm2
b: Xét ΔCAB có CF/CA=CH/CB
nên FH//AB và FH=AB/2
=>FH//AE và FH=AE
=>AEHF là hình bình hành
mà góc FAE=90 độ
nên AEHF là hình chữ nhật
Cho tam giác ABC vuông tại A, M là trung điểm BC kẻ MN vuông với AB, MQ vuông với AC
a. Chứng minh tứ giác ABMG là hình chữ nhật
b. kẻ H đối xứng với M qua Q
Xét tứ giác ANMQ có
góc ANM=góc AQM=góc QAN=90 độ
nên ANMQ là hình chữ nhật
Bài 2:
a: Xét tứ giác AHCE có
I là trung điểm chung của AC và HE
góc AHC=90 độ
Do đó: AHCE là hình chữ nhật
b: BH=CH=6cm
=>AH=8cm
\(S_{AHCE}=8\cdot6=48\left(cm^2\right)\)