Xét sự đồng biến, nghịch biến của các hàm số :
a) \(y=3x^2-8x^3\)
b) \(y=16x+2x^2-\dfrac{16}{3}x^3-x^4\)
c) \(y=x^3-6x^2+9x\)
d) \(y=x^4+8x^2+5\)
Tìm các khoảng đồng biến, nghịch biến của các hàm số
a) \(y=\dfrac{3-2x}{x+7}\)
b) \(y=\dfrac{1}{\left(x-5\right)^2}\)
c) \(y=\dfrac{2x}{x^2-9}\)
d) \(y=\dfrac{x^4+48}{x}\)
e) \(y=\dfrac{x^2-2x+3}{x+1}\)
g) \(y=\dfrac{x^2-5x+3}{x-2}\)
Xét tính đơn điệu của các hàm số :
a) \(y=\sqrt{25-x^2}\)
b) \(y=\dfrac{\sqrt{x}}{x+100}\)
c) \(y=\dfrac{x}{\sqrt{16-x^2}}\)
d) \(y=\dfrac{x^3}{\sqrt{x^2-6}}\)
Xét sự đồng biến, nghịch biến của các hàm số :
a) \(y=x-\sin x,x\in\left[0;2\pi\right]\)
b) \(y=x+2\cos x,x\in\left[\dfrac{\pi}{6};\dfrac{5\pi}{6}\right]\)
c) \(y=\sin\dfrac{1}{x},x>0\)
Xác định m để hàm số sau :
a) \(y=\dfrac{mx-4}{x-m}\) đồng biến trên từng khoảng xác định
b) \(y=\dfrac{-mx-5m+4}{x+m}\) nghịch biến trên từng khoảng xác định
c) \(y=-x^3+mx^2-3x+4\) nghịch biến trên \(\left(-\infty;+\infty\right)\)
d) \(y=x^3-2mx^2+12x-7\) đồng biến trên \(\mathbb{R}\)
Chứng minh các phương trình sau đây có nghiệm duy nhất
a) \(3\left(\cos x-1\right)+2\sin x+6x=0\)
b) \(4x+\cos x-2\sin x-2=0\)
c) \(-x^3+x^2-3x+2=0\)
d) \(x^5+x^3-7=0\)
Chứng minh phương trình :
\(x^5-x^2-2x-1=0\)
có nghiệm duy nhất
lời giải
theo phương pháp chia nhỏ xét
\(f\left(x\right)=x^5-x^2-2x-1\)
\(f'\left(x\right)=5x^4-2x-2\)
\(f''\left(x\right)=20x^3-2\)
1) xét f'(x)
\(f''\left(x\right)=0\Rightarrow x=\sqrt[3]{\dfrac{1}{10}}\Rightarrow f'\left(x\right)\)
xét hàm f'(x) nếu có chỉ có 2 nghiệm trái dấu
f''(x) \(\left\{{}\begin{matrix}f''\left(x\right)< 0\\x\le0\end{matrix}\right.\)
Vậy điểm cực đại f(x) có hoành độ xcd<0
\(\left\{{}\begin{matrix}f'\left(-1\right)=5>0\\f'\left(0\right)=-2< 0\\f'\left(1\right)=1>0\end{matrix}\right.\) vậy f'(x) có hai nghiệm \(\left[{}\begin{matrix}x_{cđ}=\left(-1,0\right)\\x_{ct}=\left(0,1\right)\end{matrix}\right.\)
Ta lại có
\(f\left(x\right)=\dfrac{x}{5}.f'\left(x\right)-\dfrac{1}{5}\left(3x^2+8x+5\right)\)
\(\Rightarrow f\left(x_{cd}\right)=-\dfrac{1}{5}\left(x^2+8x-5\right)\)
{a-b+c=0} \(\Rightarrow f\left(x_{cd}\right)\le0..khi..\left[{}\begin{matrix}x\le-\dfrac{5}{3}\\x\ge-1\end{matrix}\right.\)
Khi \(-1< x< 0\Rightarrow f\left(cđ\right)< 0\)
\(\Rightarrow f\left(x\right)\) có nghiệm duy nhất --> dpcm
p/s:
nếu làm tổng thể \(f\left(x_{xd}\right).f\left(x_{ct}\right)>0\) ra bậc bốn rất khó khăn trong việc giải BPT
Trả lời bởi ngonhuminh
Chứng minh các bất đẳng thức sau :
a) \(\tan x>\sin x;0< x< \dfrac{\pi}{2}\)
b) \(1+\dfrac{1}{2}x-\dfrac{x^2}{8}< \sqrt{1+x}< 1+\dfrac{1}{2}x\) với \(0< x< +\infty\)
Chứng minh rằng phương trình :
\(x^3-3x+c=0\)
không thể có hai nghiệm thực trong đoạn \(\left[0;1\right]\)
Xét hàm số vế trái \(f\left(x\right)=x^3-3x+c\)
Ta có: \(f'\left(x\right)=3x^2-3=3\left(x^2-1\right)\)
Hàm số liên tục trên toàn trục số và trên khoảng (0;1) thì \(f'\left(x\right)< 0\) nên hàm số nghịch biến trên [0;1]. Vậy phương trình f(x)=0 không thể có hai nghiệm trên [0; 1].
Trả lời bởi Giáo viên ToánXét sự đồng biến, nghịch biến của các hàm số:
a) \(y = 4 + 3x - x^2\) ;
b) \(y=\dfrac{1}{3} x^3 + 3x^2 - 7x - 2\) ;
c) y = x4 - 2x2 + 3 ;
d) y = -x3 + x2 - 5.
1. a) Tập xác định : D = R; y' = 3 - 2x => y' = 0 ⇔ x = \(\dfrac{3}{2}\).
Bảng biến thiên :
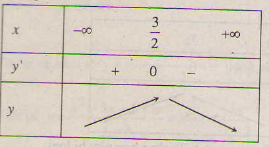
Hàm số đồng biến trên khoảng (-∞; \(\dfrac{3}{2}\)); nghịch biến trên khoảng ( \(\dfrac{3}{2}\); +∞ ).
b) Tập xác định D = R;
y'= x2 + 6x - 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên :
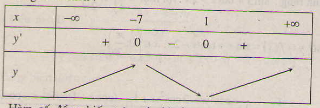
Hàm số đồng biến trên các khoảng (-∞ ; -7), (1 ; +∞) ; nghịch biến trên các khoảng (-7 ; 1).
c) Tập xác định : D = R.
y' = 4x3 - 4x = 4x(x2 - 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: tự vẽ.
Hàm số đồng biến trên các khoảng (-1 ; 0), (1 ; +∞) ; nghịch biến trên các khoảng (-∞ ; -1), (0 ; 1).
d) Tập xác định : D = R. y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = \(\dfrac{2}{3}\).
Bảng biến thiên :
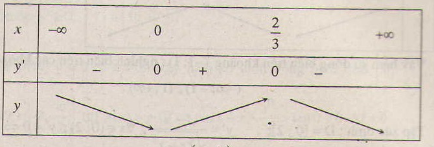
Hàm số đồng biến trên khoảng ( 0 ; \(\dfrac{2}{3}\) ) ; nghịch biến trên các khoảng (-∞ ; 0), ( \(\dfrac{2}{3}\); +∞).
Trả lời bởi qwerty
Trả lời bởi Nguyen Thuy Hoa