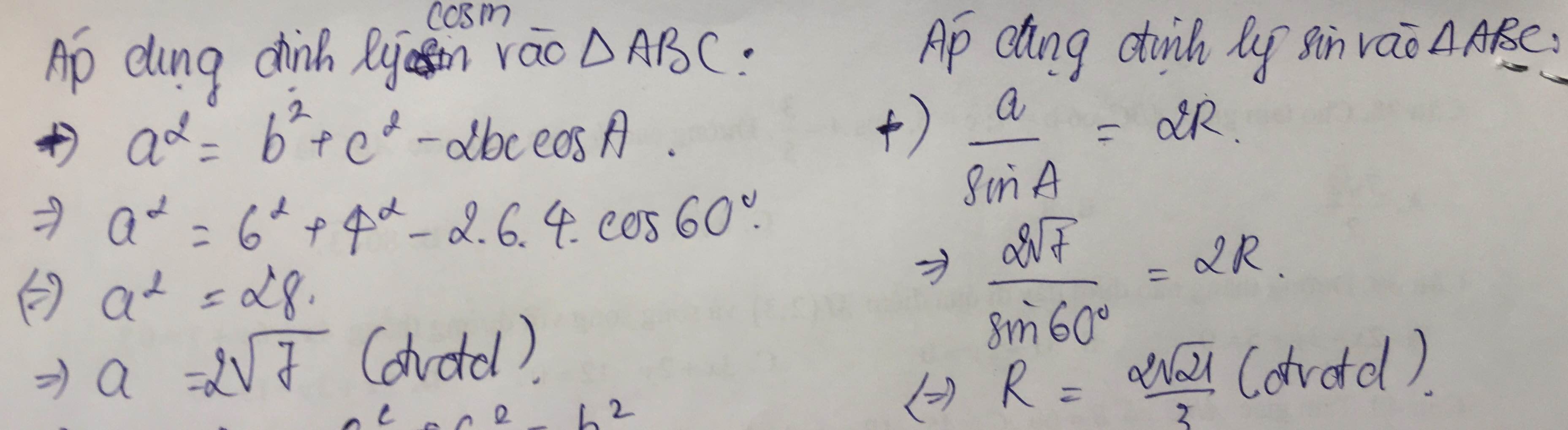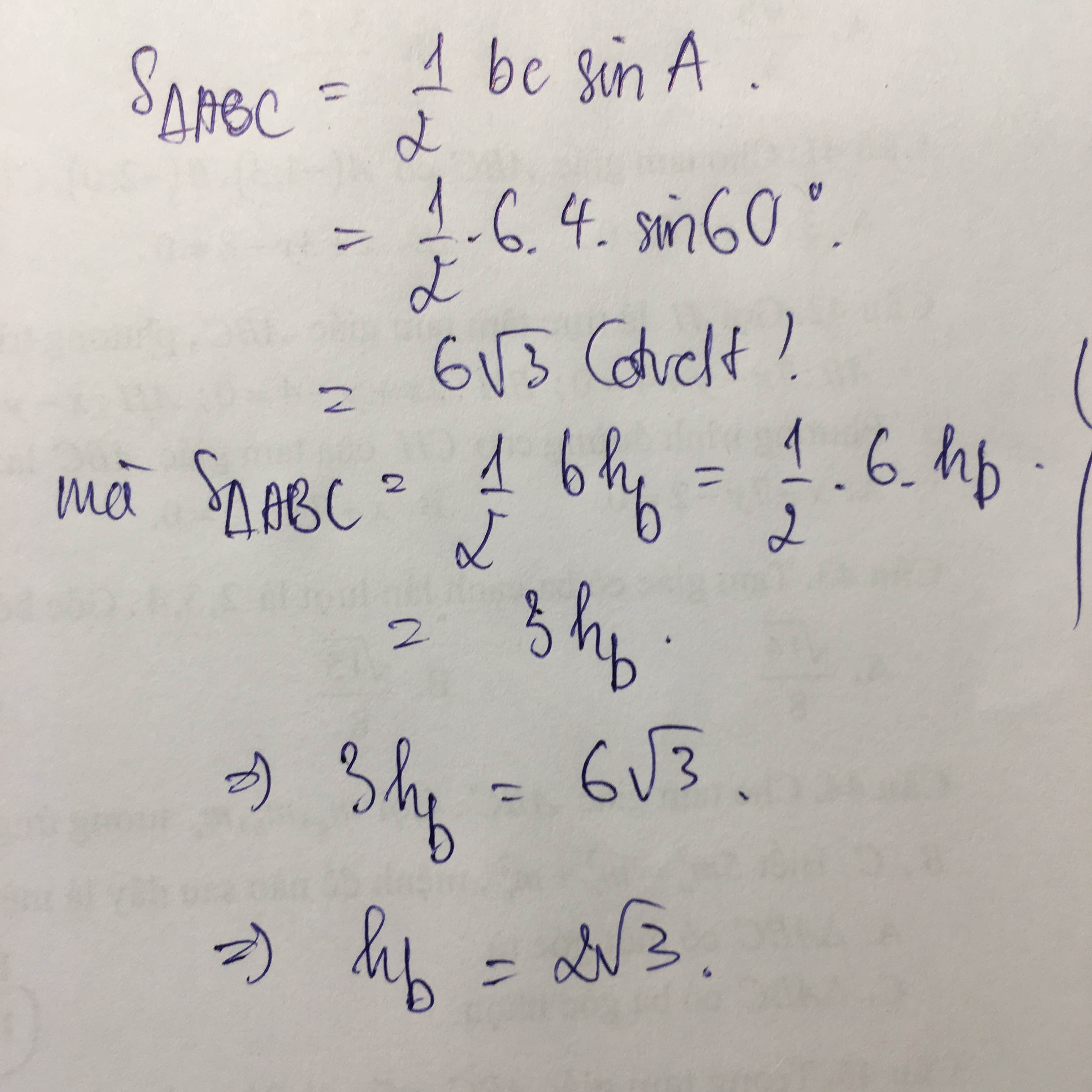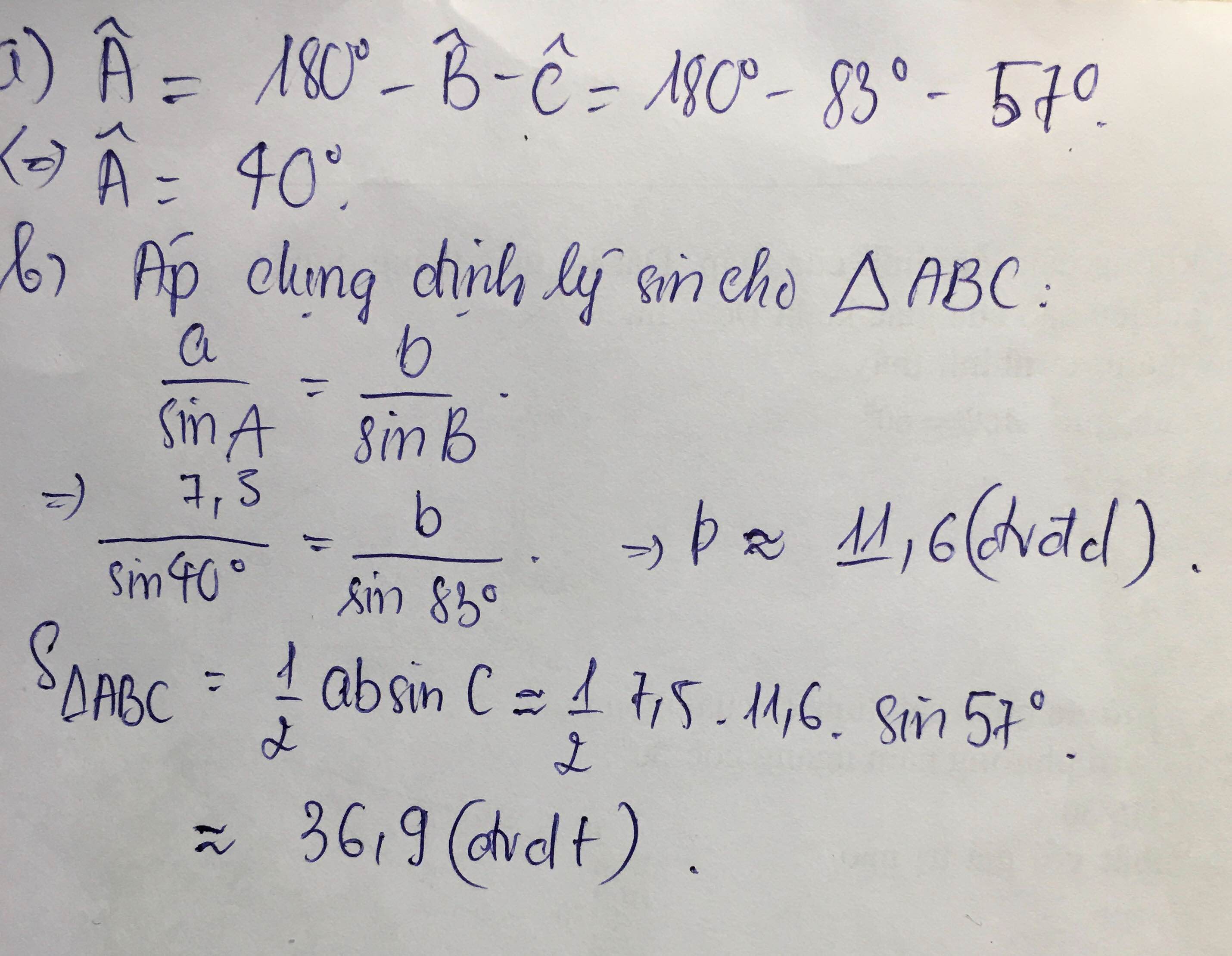Cho tam giác ABC có b = 6cm, c = 4cm, góc A = 60 độ. Tính cạnh a, bán kính đường tròn ngoại tiếp tam giác ABC, đường cao Bh của tam giác ABC
§3. Các hệ thức lượng giác trong tam giác và giải tam giác
RN
29 tháng 3 2022 lúc 8:19
Xem thêm câu trả lời
MS
18 tháng 3 2022 lúc 8:58
Cho \(\tan\alpha-5\cot\alpha+4=0.\). Tính \(A=\frac{4\sin\alpha+2\cos\alpha}{3\sin\alpha-\cos\alpha}\)
\(tana-5cota+4=0\Rightarrow tana-\dfrac{5}{tana}+4=0\)
\(\Rightarrow tan^2a+4tana-5=0\Rightarrow\left[{}\begin{matrix}tana=1\\tana=-5\end{matrix}\right.\)
\(A=\dfrac{4sina+2cosa}{3sina-cosa}=\dfrac{\dfrac{4sina}{cosa}+\dfrac{2cosa}{cosa}}{\dfrac{3sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{4tana+2}{3tana-1}=\left[{}\begin{matrix}3\\\dfrac{9}{8}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 6cm, A = 200, C = 500. Độ dài cạnh AC (làm tròn một chữ số thập phân) là
A. 7,4cm B. 6,8cm C. 8,2cm D. 7,9cm
Xem thêm câu trả lời
Cho tam giác ABC có AB = 4cm; AC = 6cm và A = 400. Độ dài cạnh BC (làm tròn một chữ số thập phân) là
A. 3,6cm B. 4,2cm C. 3,9cm D. 4,1cm
Áp dụng định lý Cosin:
\(BC^2=AB^2+AC^2-2.AB.AC.\cos A.\)
Thay: \(BC^2=4^2+6^2-2.4.6.\cos40.\\ \Rightarrow BC\approx3,9\left(cm\right).\)
\(\Rightarrow C.\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có độ dài ba cạnh lần lượt là 4cm; 5cm; 7cm . Độ dài bán kính đường tròn ngoại tiếp tam giác ABC (làm tròn một chữ số thập phân) là
A. 3,6cm B. 2,4cm C. 4,1cm D. 3,8cm
Xem thêm câu trả lời
Cho tam giác ABC có độ dài ba cạnh lần lượt là 4cm; 5cm; 7cm . Độ dài bán kính đường tròn ngoại tiếp tam giác ABC (làm tròn một chữ số thập phân) là
A. 3,6cm B. 2,4cm C. 4,1cm D. 3,8cm
Xem thêm câu trả lời
TB
10 tháng 3 2022 lúc 21:33
Cho tam giác ABC có độ dài ba cạnh lần lượt là 4cm; 5cm; 7cm . Độ dài bán kính đường tròn ngoại tiếp tam giác ABC (làm tròn một chữ số thập phân) là:
A. 3,6cm B. 2,4cm C. 4,1cm D. 3,8cm
MS
10 tháng 3 2022 lúc 21:30
Cho tam giác ABC có độ dài ba cạnh lần lượt là 4cm; 5cm; 7cm . Độ dài bán kính đường tròn ngoại tiếp tam giác ABC (làm tròn một chữ số thập phân) là:
A. 3,6cm B. 2,4cm C. 4,1cm D. 3,8cm
Xem thêm câu trả lời