Sử dụng dấu bất đẳng thức để viết các mệnh đề sau :
a) x là số dương
b) y là số không âm
c) Với mọi số thực \(\alpha,\left|\alpha\right|\) là số không âm
d) Trung bình cộng của hai số dương a và b không nhỏ hơn trung bình nhân của chúng
Sử dụng dấu bất đẳng thức để viết các mệnh đề sau :
a) x là số dương
b) y là số không âm
c) Với mọi số thực \(\alpha,\left|\alpha\right|\) là số không âm
d) Trung bình cộng của hai số dương a và b không nhỏ hơn trung bình nhân của chúng
Có thể rút ra kết luận gì về dấu của hai số a và b nếu biết :
a) \(ab>0\)
b) \(\dfrac{a}{b}>0\)
c) \(ab< 0\)
d) \(\dfrac{a}{b}< 0\)
a) Hai số a và b cùng dấu.
b) Hai số a và b cùng dấu.
c) Hai số a và b trái dấu nhau.
d) Hai số a và b trái dấu nhau.
Trả lời bởi Nguyễn Đắc ĐịnhTrong các suy luận sau, suy luận nào đúng ?
(A) \(\left\{{}\begin{matrix}x< 1\\y< 1\end{matrix}\right.\)\(\Rightarrow xy< 1\) (B) \(\left\{{}\begin{matrix}x< 1\\y< 1\end{matrix}\right.\)\(\Rightarrow\dfrac{x}{y}< 1\)
(C) \(\left\{{}\begin{matrix}0< x< 1\\y< 1\end{matrix}\right.\) \(\Rightarrow xy< 1\) (D)\(\left\{{}\begin{matrix}x< 1\\y< 1\end{matrix}\right.\) \(\Rightarrow x-y< 0\)
Suy luận D là chính xác
Trả lời bởi Nguyễn Quang ĐịnhKhi cân một vật với độ chính xác đến 0,05kg, người ta cho biết kết quả là 26,4kg. Hãy chỉ ra khối lượng thực của vật đó nằm trong khoảng nào ?
Khối lượng thực của vật nằm trong khoảng:
(26,4 - 0,05; 26,4 - 0,05) kg
hay (26,35; 26,35) kg
Trả lời bởi Nguyễn Đắc ĐịnhTrên cùng một mặt phẳng tọa độ, hãy vé đồ thị hai hàm số \(y=f\left(x\right)=x+1\) và \(y=g\left(x\right)=3-x\) và chỉ ra các giá trị nào của x thỏa mãn :
a. \(f\left(x\right)=g\left(x\right)\)
b. \(f\left(x\right)>g\left(x\right)\)
c. \(f\left(x\right)< g\left(x\right)\)
Kiểm tra lại kết quả bằng cách giải phương trình, bất phương trình
Cho a, b, c là các số dương. Chứng minh rằng :
\(\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}\ge6\)
Ta có a,b,c > 0
Áp dụng bất đẳng thức Cô-si : \(a+b\ge2\sqrt{ab}\)
và \(a+b+c\ge3\sqrt[3]{abc}\)
Ta được: Vế trái \(\ge\dfrac{2\sqrt{ab}}{c}+\dfrac{2\sqrt{bc}}{a}+2\dfrac{\sqrt{ac}}{b}\)
\(\ge3\sqrt[3]{\dfrac{2\sqrt{ab}\times2\sqrt{bc}\times2\sqrt{ac}}{abc}}\)
\(\ge3\sqrt[3]{\dfrac{8\sqrt{a^2b^2c^2}}{abc}\ge6}\) (Đpcm)
Vậy: \(\dfrac{a+b}{c}+\dfrac{b+c}{a}+\dfrac{c+a}{b}\ge6\)
Trả lời bởi Nguyễn Quốc Anh
Điều kiện của một bất phương trình là gì ? Thế nào là hai bất phương trình tương đương ?
Ta gọi các điều kiện của ẩn sốx để các biểu thức f(x) và g(x) có nghĩa là điều kiện xác định của bất phương trình (hay gọi tắt là điều kiện của bất phương trình).
- Hai bất phương trình được gọi là tương đương khi chúng có cùng tập nghiệm
Trả lời bởi Nguyễn Quang ĐịnhNêu quy tắc biểu diễn hình học tập nghiệm của bất phương trình \(ax+by\le c\)
+ Ta vẽ đường thẳng (d): ax+by=c
+ Chọn điểm M(x0,y0) ∉ (d) (thường là điểm (0,0)) và tính giá trị ax0 + by0
+ Nếu ax0 + by0>c thì nửa mặt phẳng bờ (d) chứa M(x0,y0) là tập hợp các điểm mà tọa độ của nó là nghiệm của bất phương trình.
+ Nếu ax0 + by00,y0) là tập hợp các điểm có tọa độ là nghiệm của bất phương trình.
Phát biểu định lí về dấu của tam thức bậc hai
Định lí. Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0)
có biệt thức ∆ = b2 – 4ac.
- Nếu ∆ < 0 thì với mọi x, f(x) có cùng dấu với hệ số a.
- Nếu ∆ = 0 thì f(x) có nghiệm kép x = , với mọi x ≠
, f(x) có cùng dấu với hệ số a.
- Nếu ∆ > 0, f(x) có 2 nghiệm x1, x2 (x1 < x2) và luôn cùng dấu với hệ số a với mọi x ngoài đoạn [x1; x2] và luôn trái dấu với hệ số a với mọi x trong đoạn (x1; x2).
Trả lời bởi Trần Thị Bích TrâmCho \(a>0,b>0\). Chứng minh rằng :
\(\dfrac{a}{\sqrt{b}}+\dfrac{b}{\sqrt{a}}\ge\sqrt{a}+\sqrt{b}\)
Đặt \(x=\sqrt{a};y=\sqrt{b}\left(x,y>0\right)\) ta có:
\(\dfrac{x^2}{y}+\dfrac{y^2}{x}\ge x+y\left(1\right)\), vậy ta cần chứng minh \(\left(1\right)\) đúng
Áp dụng BĐT Cauchy-Schwarz dạng Engel ta có:
\(\dfrac{x^2}{y}+\dfrac{y^2}{x}\ge\dfrac{\left(x+y\right)^2}{x+y}=x+y\)
Trả lời bởi Lightning Farron
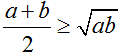
Trả lời bởi Nguyễn Đắc Định