a. Bằng cách sử dụng hằng đẳng thức \(a^2-b^2=\left(a-b\right)\left(a+b\right)\) hãy xét dấu
\(f\left(x\right)=x^4-x^2+6x-9\)
và
\(g\left(x\right)=x^2-2x-\dfrac{4}{x^2-2x}\)
b. Hãy tìm nghiệm nguyên của bất phương trình sau :
\(x\left(x^3-x+6\right)>9\)
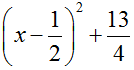
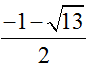
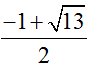
Trả lời bởi Nguyễn Đắc Định