Cho hình chóp tam giác đều S.ABC có SH là đường cao. Chứng minh \(SA\perp BC\) và \(SB\perp AC\) ?
Bài 4: Hai mặt phẳng vuông góc
SK
Hướng dẫn giải
Thảo luận (1)
SK
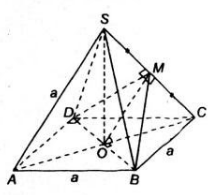
Cho hình chóp tứ giác đều S.ABCD có các cạnh bên và các cạnh đáy đều bằng a. Gọi O là tâm của hình vuông ABCD.
a) Tính độ dài đoạn thẳng SO
b) Gọi M là trung điểm của đoạn SC. Chứng minh hai mặt phẳng (MBD) và (SAC) vuông góc với nhau
c) Tính độ dài đoạn OM và tính góc giữa hai mặt phẳng (MBD) và (ABCD)
Hướng dẫn giải
Thảo luận (1)
SK
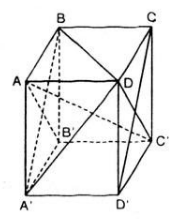
Cho lập phương ABCD.A'B'C'D'. Chứng minh rằng :
a) Mặt phẳng (AB'C'D) vuông góc với mặt phẳng (BCD'A')
b) Đường thẳng AC' vuông góc với mặt phẳng (A'BD)
Hướng dẫn giải
Thảo luận (1)
SK
Tính độ dài đường chéo của một hình lập phương cạnh a ?
Hướng dẫn giải
Thảo luận (1)
SK
Cho hình chóp S.ABCD có đáy ABCD là một hình thoi cạnh a và SA=SB=SC=a. Chứng minh rằng :
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD)
b) Tam giác SBD là tam giác vuông
Hướng dẫn giải
Thảo luận (1)
SK
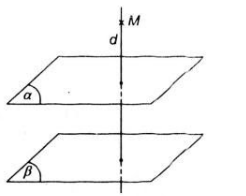
Cho hai mặt phẳng left(alpharight),left(betaright) cắt nhau và một điểm M không thuộc left(alpharight) và không thuộc left(betaright). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với left(alpharight),left(betaright). Nếu left(alpharight) song song với left(betaright) thì kết quả trên sẽ thay đổi như thế nào ?
Đọc tiếp
Cho hai mặt phẳng \(\left(\alpha\right),\left(\beta\right)\) cắt nhau và một điểm M không thuộc \(\left(\alpha\right)\) và không thuộc \(\left(\beta\right)\). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với \(\left(\alpha\right),\left(\beta\right)\). Nếu \(\left(\alpha\right)\) song song với \(\left(\beta\right)\) thì kết quả trên sẽ thay đổi như thế nào ?
Hướng dẫn giải
Thảo luận (1)
SK
Cho hai mặt phẳng left(alpharight) và left(betaright) vuông góc với nhau. Người ta lấy trên giao tuyến Delta của hai mặt phẳng đó hai điểm A và B sao cho AB 8 cm. Gọi C là một điểm trên mặt phẳng left(alpharight) và D là một điểm trên left(betaright) sao cho AC và BD cùng vuông góc với giao tuyến Delta và AC 6cm, BD 24cm. Tính độ dài đoạn CD ?
Đọc tiếp
Cho hai mặt phẳng \(\left(\alpha\right)\) và \(\left(\beta\right)\) vuông góc với nhau. Người ta lấy trên giao tuyến \(\Delta\) của hai mặt phẳng đó hai điểm A và B sao cho AB = 8 cm. Gọi C là một điểm trên mặt phẳng \(\left(\alpha\right)\) và D là một điểm trên \(\left(\beta\right)\) sao cho AC và BD cùng vuông góc với giao tuyến \(\Delta\) và AC = 6cm, BD = 24cm. Tính độ dài đoạn CD ?
Hướng dẫn giải
Thảo luận (1)
SK
Cho 3 mặt phẳng left(alpharight),left(betaright),left(gammaright). Mệnh đề nào sau đây đúng ?
a) Nếu left(alpharight)perpleft(betaright) và left(alpharight)backslashbackslashleft(gammaright) thì left(betaright)perpleft(gammaright)
b) Nếu left(alpharight)perpleft(betaright) và left(alpharight)perpleft(gammaright) thì left(betaright)backslashbackslashleft(gammaright)
Đọc tiếp
Cho 3 mặt phẳng \(\left(\alpha\right),\left(\beta\right),\left(\gamma\right)\). Mệnh đề nào sau đây đúng ?
a) Nếu \(\left(\alpha\right)\perp\left(\beta\right)\) và \(\left(\alpha\right)\backslash\backslash\left(\gamma\right)\) thì \(\left(\beta\right)\perp\left(\gamma\right)\)
b) Nếu \(\left(\alpha\right)\perp\left(\beta\right)\) và \(\left(\alpha\right)\perp\left(\gamma\right)\) thì \(\left(\beta\right)\backslash\backslash\left(\gamma\right)\)
Hướng dẫn giải
Thảo luận (1)
a) Đúng, vì nếu gọi m là đường thẳng vuông góc với β và n là đường thẳng vuông góc với hai mặt phẳng song song α, γ thì góc (m, n) = (β, α) = (β, γ), mà β ⊥ α nên β ⊥ γ.
b) Sai, vì hai mặt phẳng (β), (γ) cùng vuông góc với mp(α) có thể song song hoặc cắt nhau.
Trả lời bởi Quang Duy
SK
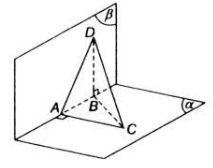
Trong mặt phẳng left(alpharight) cho tam giác ABC vuông ở B. Một đoạn thẳng AD vuông góc với left(alpharight) tại A. Chứng minh rằng :
a) widehat{ABD} là góc giữa hai mặt phẳng (ABC) và (DBC)
b) Mặt phẳng (ABD) vuông góc với mặt phẳng (BDC)
c) HK// BC với H và K lần lượt là giao điểm của DB và DC với mặt phẳng (P) đi qua A và vuông gcs với DB
Đọc tiếp
Trong mặt phẳng \(\left(\alpha\right)\) cho tam giác ABC vuông ở B. Một đoạn thẳng AD vuông góc với \(\left(\alpha\right)\) tại A. Chứng minh rằng :
a) \(\widehat{ABD}\) là góc giữa hai mặt phẳng (ABC) và (DBC)
b) Mặt phẳng (ABD) vuông góc với mặt phẳng (BDC)
c) HK// BC với H và K lần lượt là giao điểm của DB và DC với mặt phẳng (P) đi qua A và vuông gcs với DB
Hướng dẫn giải
Thảo luận (1)
SK
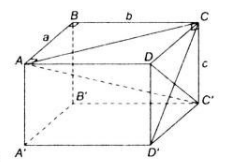
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a; BC = b; CC'=c
a) Chứng minh rằng mặt phẳng (ADC'B') vuông góc với mặt phẳng (ABB'A')
b) Tính độ dài đường chéo AC' theo a, b, c
Hướng dẫn giải
Thảo luận (1)



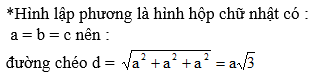
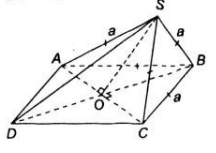



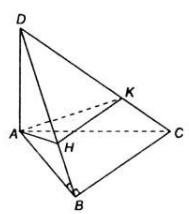


Hình chóp tam giác đều S.ABC có đáy là tam giác đều ABC và chân đường cao trùng với tâm của đáy. H là tâm của tam giác đều ABC
● AH ⊥ BC
Mà AH là hình chiếu của SA trên (ABC)
⇒BC ⊥SA.
● Tương tự AC ⊥ BH.
BH là hình chiếu của SB trên (ABC)
⇒AC ⊥ SB.
Trả lời bởi Quang Duy