Cho hai đường thẳng phân biệt a, b và mặt phẳng \(\left(\alpha\right)\). Các mệnh đề sau đây đúng hay sai ?
a) Nếu a // \(\left(\alpha\right)\) và \(b\perp\left(\alpha\right)\) thì \(a\perp b\)
b) Nếu a // \(\left(\alpha\right)\) và \(b\perp a\) thì \(b\perp\left(\alpha\right)\)
c) Nếu a // \(\left(\alpha\right)\) và b // \(\left(\alpha\right)\) thì b // a
d) Nếu a \(\perp\) \(\left(\alpha\right)\) và\(b\perp a\) thì b // (\(\alpha\))
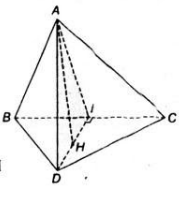

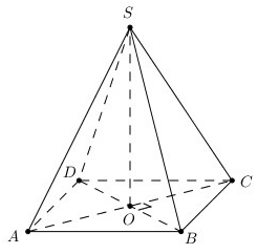


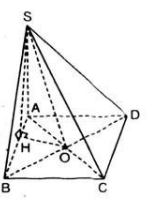


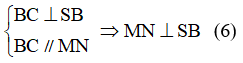


a) Đúng
b) Sai
c) Sai
d) Sai
Trả lời bởi Lưu Hạ Vy