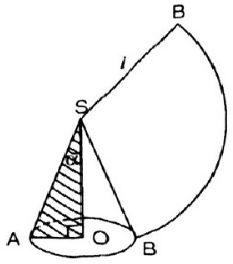
Viết công thức tính nửa góc ở đỉnh của một hình nón (góc \(\alpha\) của tam giác vuông AOS - hình 99) sao cho diện tích mặt khai triển cảu mặt nón bằng một phần tư diện tích của hình tròn (bán kính SA).
Hình khai triển của mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là 16 cm, số đo cung là 120o. Tan của nửa góc ở đỉnh của hình nón là:
(A) \(\dfrac{\sqrt{2}}{4};\) (B) \(\dfrac{\sqrt{2}}{2};\) (C) \(\sqrt{2};\) (D) \(2\sqrt{2};\)
Hãy chọn kết quả đúng.
Bài 24. Hình khai triển mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là 16cm, số đo cung là 1200. Tan của góc ở đỉnh hìn nón là:
(A) (B)
(C)
(D) 2
Giải:
Đường sinh của hình nón là l = 16. Độ dài cung AB của đường tròn chưa hình quạt là , chu vi đáy bằng suy ra r = 2πr suy r =
Trong tam giác vuông AOS có:
tg(a) = =
Trả lời bởi Thien Tu Borum
Hình khai triển của mặt xung quanh của một hình nón là một hình quạt. Nếu bán kính hình quạt là 16 cm, số đo cung là 120o thì độ dài đường sinh của hình nón là:
(A) 16 cm; (B) 8 cm; (C) \(\dfrac{16}{3}\) cm;
(D) 4 cm; (E) \(\dfrac{16}{5}\) cm.
Hãy chọn kết quả đúng.
Giải:
Theo bài 16 thì bán kính đường tròn chứa hình quạt độ dài bằng đường sinh của hình nón.
Đầu bài cho bán kính hình tròn chưa hình quạt là 16 cm nên độ dài đường sinh là 16 cm.
Vậy chọn A
Trả lời bởi Thien Tu Borum
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (OA = OB). Hãy so sánh tổng các thể tích của hai hình nón và thể tích của hình trụ.
Giải:
Chiều cao của hình nón là:
Thể tích của hai hình nón là:
2Vnón =
Thể tích của hình trụ:
Vtrụ = πR2h
Nên
Trả lời bởi Thien Tu Borum
Hãy điền đầy đủ các ô trống ở bảng sau (xem hình 96):
| Bán kính đáy r (cm) | Đường kính đáy d (cm | Chiều cao h (cm) | Độ dài đường sinh l (cm) | Thể tích V (cm3) |
| 10 | 10 | |||
| 10 | 10 | |||
| 10 | 1000 | |||
| 10 | 1000 | |||
| 10 | 1000 |
Bài 20. Hãy điền đủ vào các ô trống ở bảng sau (xem hình 96)
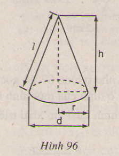
Giải:
Dòng thứ nhất:
d = 2r = 1.10 = 20(cm)
l = (cm)
V = (cm3)
Dòng thứ hai: r= = 5 (cm)
l = (cm)
V = (cm3)
Tương tự cho dòng 3,4 ta được bảng sau:
Trả lời bởi Thien Tu Borum
Hình ABCD khi quay quanh BC thì tạo ra:
(A) Một hình trụ; (B) Một hình nón; (C) Một hình nón cụt;
(D) Hai hình nón; (E) Hai hình trụ.
Hãy chọn câu trả lời đúng.
Giải:
Gọi O là giao điểm của BC và AD
Khi quay hình ABCD quanh BC có nghĩa là tam giác vuông OBA quanh OB và tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ tạo ra 2 hình nón.
Vậy chọn D
Trả lời bởi Thien Tu Borum
Cắt mặt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết basnk ính hình quạt tròn bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.
Quan sát hình 94 và tính số đo cung của hình quạt tròn.
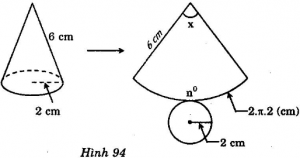
Giải:
Độ dài l của cung hình quạt tròn bán kính 6 cm bằng chu vi đáy của hình nón:
l = 2 π.2 = 4 π
Áp dụng công thức tính độ dài cung trong x0 ta có:
l =
Suy ra: x0 = = 1200
Trả lời bởi Thien Tu Borum
Một hình nón được đặt vào bên trong một hình lập phương như hình vẽ (cạnh của hình lập phương bằng 1) (h.93). Hãy tính:
a) Bán kính đáy của hình nón.
b) Độ dài đường sinh.
Giải
a) Có đường tròn đáy của hình nón nội tiếp trong hình vuông của một mặt hình lập phương. Do đó bán kính của đáy hình nón bằng một nửa cạnh hình lập phương và bằng 0,5.
b) Đỉnh cua hình nón tiếp xúc với một mặt của hình lập phương nên đường cao của hình nón bằng với cạnh của hình lập phương vàng bằng 1.
Theo định lí pytago, độ dài đường sinh của hình nón là :
l = =
Trả lời bởi Thien Tu Borum
Khi quay tam giác vuông để tạo ra một hình nón như ở hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là 30o, độ dài đường kính là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
iải:
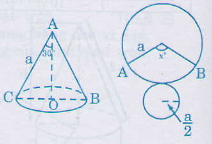
Theo đề bài: góc ở đỉnh cả hình nón là 600 nên suy ra đường kính của đường tròn đáy của một hình nón bằng a(do ∆ABC đều). Vậy bán kính đáy của hình nón là
Đường sinh của hình nón là a.
Độ dài cung hình quạt n0, bán kính a bằng chu vi đáy là a.
Độ dài cung hình quạt trong n0, bán kính a bằng chu vi đáy hình tròn nên ta có:
Suy ra n0 = 1800.
Trả lời bởi Thien Tu Borum
Cái mũ của chú hề với các kích thước cho theo hình vẽ (h. 97). Hãy tính tổng diện tích vải cần có để làm lên cái mũ (không kể riềm, mép, phần thừa).
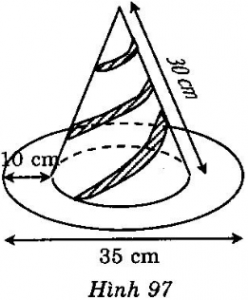
Giải:
Diện tích vải cần có để làm nên cái mũ diện tích xung quanh của hình nón và diện tích vành nón.
(cm)
Vậy diện tích vải cần có là:
S = Sxq + SVành nón = 706,5 + 785 = 1491,5 (cm2)
Trả lời bởi Thien Tu Borum
Giải:
Diện tích hình quạt :
Diện tích xung quanh của hình nón: Sxq = π.r.l
Theo đầu bài ta có: Sxq= Sq => π.r.l=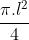
Vậy l = 4r
Suy ra sin(a) =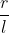
= 0,25
Vậy a = 14o28’
Trả lời bởi Thien Tu Borum