Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón, hình nón cụt

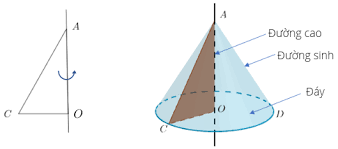
Khi quay một tam giác vuông \(AOC\) một vòng quanh cạnh góc vuông \(OA\) cố định thì được một hình nón.

• Cạnh \(OC\) tạo nên đáy của hình nón, là một hình tròn tâm \(O\).

• Cạnh \(AC\) quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn \(AD\) là một đường sinh.

• \(A\) là đỉnh và \(AO\) là đường cao của hình nón.

2. Diện tích xung quanh của hình nón

Cắt mặt xung quanh của hình nón dọc theo một đường sinh của nó rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình nón là một hình quạt tròn. Hình này có tâm là đỉnh hình nón, bán kính là độ dài đường sinh, độ dài cung bằng độ dài đường tròn đáy.

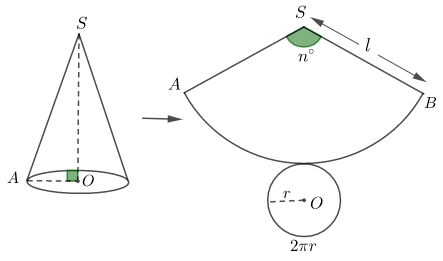
Gọi bán kính đáy hình nón là \(r\), độ dài đường sinh là \(l\).

• Độ dài của cung hình quạt tròn là: \(\dfrac{\pi ln}{180}\).
• Độ dài đường tròn đáy của hình nón là \(2\pi r\)

\(\Rightarrow\dfrac{\pi ln}{180}=2\pi r\Rightarrow r=\dfrac{ln}{360}\).

• Diện tích hình quạt tròn là: \(S=\dfrac{\pi l^2n}{360}=\pi l.\dfrac{ln}{360}=\pi rl\).

Tổng quát:

• Diện tích xung quanh hình nón là:

\(S_{xq}=\pi rl\)

• Diện tích toàn phần hình nón là:

\(S_{tp}=\pi rl+\pi r^2\)

Ví dụ: Tính diện tích xung quanh hình nón có chiều cao \(h=5cm\), độ dài đường sinh \(l=13cm\)?

Giải:

Ta có: \(h^2+r^2=l^2\Rightarrow r=\sqrt{l^2-h^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)

\(\Rightarrow\) Diện tích xung quanh hình nón là: \(S_{xq}=\pi rl=\pi.12.13=156\left(cm^2\right)\).

3. Thể tích hình nón

Bằng thực nghiệm, ta thấy:

Thể tích hình nón có bán kính đáy \(r\), chiều cao \(h\) là:

\(V=\dfrac{1}{3}\pi r^2h\)

4. Hình nón cụt

- Cắt hình nón bởi một mặt phẳng song song với đáy thì phần mặt phẳng nằm trong hình nón là một hình tròn. 

- Phần hình nón nằm giữa mặt phẳng nói trên và mặt đáy là một hình nón cụt.

Ví dụ: Chụp đèn, bình hoa, ... trong các hình dưới đây là hình nón cụt

5. Diện tích xung quanh và thể tích hình nón cụt

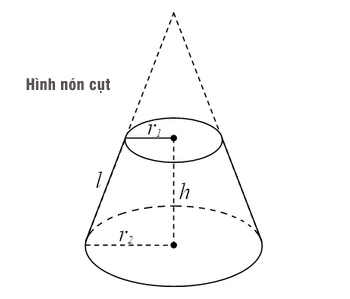
Cho hình nón cụt có bán kính các đáy là \(r_1,r_2\); độ dài đường sinh là \(l\); chiều cao là \(h\).

Nhận thấy, diện tích xung quanh (thể tích) hình nón cụt bằng hiệu của diện tích xung quanh (thể tích) hai hình nón lớn và nhỏ.

Từ đó, ta có kết luận:

• Diện tích xung quanh hình nón cụt:

\(S_{xq}=\pi\left(r_1+r_2\right)l\)

• Thể tích hình nón cụt: 

\(V=\dfrac{1}{3}\pi h\left(r_1^2+r_2^2+r_1r_2\right)\)