Nếu thể tích của một hình cầu là \(113\dfrac{1}{7}cm^3\) thì trong các kết quả sau đây, kết quả nào là bán kính của nó (lấy \(\pi\approx\dfrac{22}{7}\) )?
(A) 2 cm; (B) 3 cm; (C) = 5 cm; (D) 6 cm.
Hãy chọn kết quả đúng.
Hãy điền vào các ô trống ở bảng sau:
| Bán kính hình cầu | 0,3 mm | 6,21 dm | 0,283 m | 100 km | 6 hm | 50 dam |
| Diện tích mặt cầu | ||||||
| Thể tích hình cầu |
Giải
ÁP dụng công thức tính diện tích mặt cầu: S= 4πR2
và công thức tính thể tích mặt cầu: V = πR3
Thay bán kính mặt cầu vào ta tính được bảng sau:
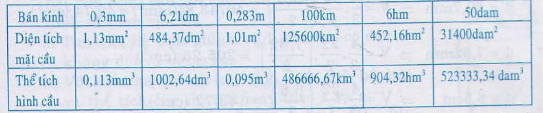
Trả lời bởi Thien Tu Borum
Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r, chiều cao 2r (đơn vị :cm). Người ta khoét rộng hai nửa hình cầu như hình 108. Hãy tính diện tích bề mặt của khối gỗ còn lại (diện tích cả ngoài lẫn trong).
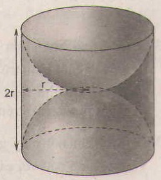
Giải:
Diện tích phần cần tính gồm diện tích xung quanh hình trụ bán kính đường tròn đáy là r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r(cm).
Diện tích xung quanh của hình trụ:
Diện tích mặt cầu:
Diện tích cần tính là: +
=
Trả lời bởi Thien Tu Borum
Dụng cụ thể thao:
Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau (làm tròn kết quả đền chữ số thập phân thứ hai):
| Loại bóng | Quả bóng gôn | Quả khúc côn cầu | Quả ten-nít | Quả bóng bàn | Quả bi-a |
| Đường kính | 42,7 mm | 6,5 cm | 40 mm | 61 mm | |
| Độ dài đường tròn lớn | 23 cm | ||||
| Diện tích | |||||
| Thể tích |
Giải:
Dòng thứ nhất: Từ C = π.d => d = =
= 7,32
Dòng thứ hai: Áp dụng công thức C = π.d, thay số vào ta được
d = 42,7 mm => C = .42,7 = 134,08 mm
d = 6,6 cm => C = .6,6 = 20,41 cm
d = 40 mm => C = . 40 = 125,6 mm
d = 61 mm => C = . 61 = 191,71 mm
Dòng thứ ba: ÁP dụng công thức S = S = πd2, thay số vào ta được:
d = 42,7 mm => S= .42,72 = 5730,34 (mm2) ≈ 57,25 (cm2)
d = 6,5 cm => S= .6,52 = 132,65 (cm2)
d = 40 mm => S= .402 = 5024 (mm2)
d = 61 mm => S= .612 = 11683,94 (mm2)
Dòng thứ 4: áp dụng công thức V = πR3 , thay số vào ta được các kết quả ghi vào bảng dưới đây:
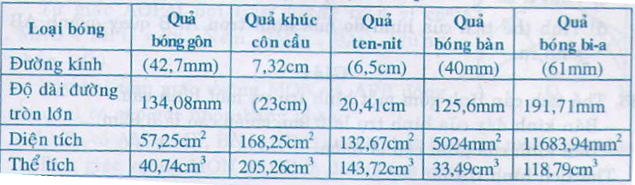
Trả lời bởi Thien Tu Borum
Khinh khí cầu của nhà Mông-gôn-fi-ê.
Ngày 4 - 6 - 1783, anh em nhà Mông-gôn-fi-ê (người Pháp) phát minh ra khinh khí cầu dùng không khí nóng. Coi khinh khí cầu này là một quả cầu có đường kính 11m. Hãy tính diện tích mặt khinh khí cầu đó, (làm tròn kết quả đến chữ số thập phân thứ hai).
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (h 110).
Hãy tính thể tích của bồn chứa theo các kích thước cho trên hình vẽ.
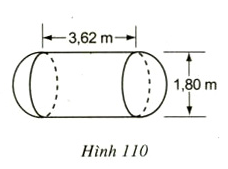
Giải:
Thể tích cần tính gồm một hình trụ và một hình cầu.
- Bán kính đáy của hình trụ là 0,9m, chiều cao là 3,62m.
- Bán kính của hình cầu là 0,9 m
Thể tích của hình trụ là :
Vtrụ = πr2h = 3,14 (0,9)2.3,62= 9,215 (m3)
Thể tích của hình cầu là:
Vcầu= πR3 =
3,14(0,9)3 = 3,055 (m3)
Thể tích của bồn chứa xăng:
V= V trụ + V cầu = 9,215 + 3,055 = 12,27 (m3)
Trả lời bởi Thien Tu Borum
Một chi tiết máy gồm một hình trụ và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị cm).
a) Tìm một hệ thức giữa x và h khi AA' có độ dài không đổi và bằng 2a.
b) Với điều kiện ở a), hãy tính diện tích bề mặt và thể tích của chi tiết máy theo x và a.
-0128.jpg)
Giải:
a) Ta có h + 2x = 2a
b) - Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính đáy là x, chiều cao là h và diện tích mặt cầu có bán kính là x.
- Diện tích xung quanh của hình trụ: Strụ = 2πxh
- Diện tích mặt cầu: Sc= 4πx2
Nên diện tích bề mặt của chi tiết máy là:
S = Strụ + Sc = 2πxh + 4πx2 = 2πx(h+2x) = 4πax
Thể tích cần tình gồm thể tích hình trù và thể tích hình cầu. Ta có:
Vtrụ = πx2h
Vcầu = V = πx3
Nên thể tích của chi tiết máy là:
V = Vtrụ + Vcầu = πx2h + πx3
= 2πx2a - (2/3)πx3
Trả lời bởi Thien Tu Borum
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến vởi nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
b) Chứng minh \(AM.BN=R^2.\)
c) Tính tỉ số \(\dfrac{S_{MON}}{S_{APB}}\) khi \(AM=\dfrac{R}{2}.\)
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Giải:
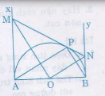
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3
a) Trong hình 102, cho A là giao điểm của đường tròn \(\left(0;6\right)\) với tia \(90^0\) và kí hiệu là \(A\left(6;90^0\right)\). Tương tự B là giao điểm của đường tròn \(\left(0;3\right)\) với tia \(150^0\) và kí hiệu là \(B\left(3;150^0\right)\). Hãy đánh dấu các điểm \(C\left(6;210^0\right),D\left(3;30^0\right),E\left(6;330^0\right)\) trên hình 102
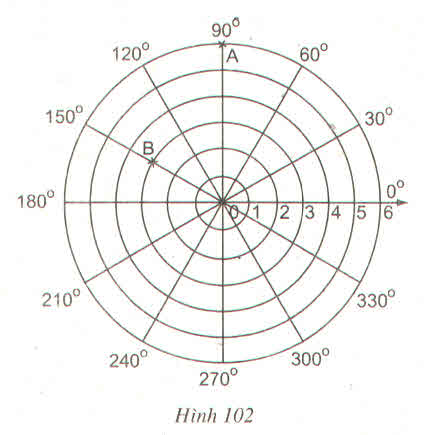
b) Nối AB, BC, AD, DE và BD em thấy hình gì ?
Trong nửa hình cầu (h.103) có \(OR=x\left(cm\right);\widehat{TOS}=45^0\)
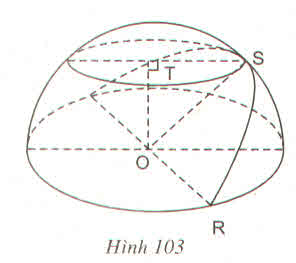
Độ dài đoạn ST nhận giá trị nào trong các giá trị sau :
(A) \(x\left(cm\right)\) (B) \(\sqrt{2}x\left(cm\right)\)
(C) \(\dfrac{x}{\sqrt{2}}\left(cm\right)\) (D) \(2x\left(cm\right)\)
Từ tam giác vuông TOS, ta có \(ST=\dfrac{x}{\sqrt{2}}\left(cm\right)\)
Vậy ta chọn (C)
Trả lời bởi Nguyen Thuy Hoa
Bài 30 Nếu thể tích của một hình cầu là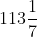
thì trong các kết quả sau đây, kết quả nào là bán kính của nó(lấy π= 22/7)?
(A) 2 cm (B) 3 cm (C) 5 cm (D) 6 cm ;
(E) Một kết quả khác.
Giải:
Từ công thức: V =
πR3 =>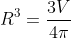 
Thay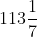
và π= 22/7 vào ta được
R3 = 27
Suy ra: R = 3
Vậy chọn B) 3cm
Trả lời bởi Thien Tu Borum