Bài 1: Hình trụ - Diện tích xung quanh và thể tích hình trụ
Nội dung lý thuyết
Các phiên bản khác1. Hình trụ
Cho hình chữ nhật \(ABCD\). Khi quay hình chữ nhật này một vòng quanh cạnh \(CD\) cố định, ta được một hình trụ.
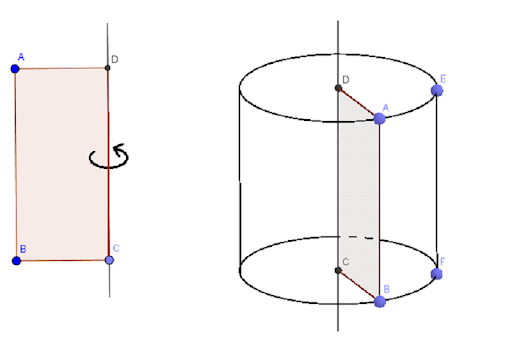
- \(DA\) và \(CB\) quét nên hai đáy của hình trụ. Đó là hai hình tròn bằng nhau, nằm trên hai mặt phẳng song song, có tâm là \(D\) và \(C\).
- Cạnh \(AB\) quét nên mặt xung quanh của hình trụ. Mỗi vị trí của \(AB\) được gọi là một đường sinh, ví dụ \(EF\) là một đường sinh.
- Các đường sinh vuông góc với hai mặt phẳng đáy. Độ dài đường sinh là chiều cao hình trụ.
- \(DC\) gọi là trục của hình trụ.
Ví dụ: Lon nước ngọt, cây nến, đường ống nước, cuộn băng dính, ... là những vật có dạng hình trụ.
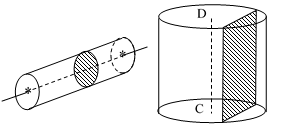
2. Cắt hình trụ bởi một mặt phẳng
- Khi cắt hình trụ bởi một mặt phẳng song song với đáy, phần mặt phẳng nằm trong hình trụ (mặt cắt) là một hình tròn bằng hình tròn đáy.
- Khi cắt hình trụ bởi một mặt phẳng song song với trục \(DC\), mặt cắt này là một hình chữ nhật. Hình chữ nhật này có một kích thước bằng chiều cao hình trụ.
3. Diện tích xung quanh của hình trụ
Từ một hình trụ, ta cắt rời hai đáy, rồi cắt dọc theo đường sinh \(AB\) của mặt xung quanh và trải phẳng ra, ta được hình khai triển mặt xung quanh của hình trụ là một hình chữ nhật. Hình chữ nhật này có một cạnh bằng chu vi hình tròn đáy, cạnh còn lại là chiều cao hình trụ.

Gọi bán kính đáy của hình trụ là \(r\); độ dài đường sinh (chiều cao) hình trụ là \(h\), ta có:
- Chiều dài hình chữ nhật bằng chu vi hình tròn đáy hình trụ và bằng: \(2\pi r\).
- Từ đó, diện tích hình chữ nhật là: \(2\pi rh\).
- Tổng diện tích hình chữ nhật và diện tích 2 hình tròn đáy là: \(2\pi rh+2\pi r^2\).
Tổng quát:
- Diện tích xung quanh của hình trụ là: \(S_{xq}=2\pi rh\).
- Diện tích toàn phần của hình trụ là: \(S_{tp}=2\pi rh+2\pi r^2\).
Như vậy, muốn tính diện tích xung quanh, diện tích toàn phần của hình trụ, ta cần tìm bán kính đáy và chiều cao của nó. Ngược lại, ta cũng có thể tìm ra bán kính đáy và chiều cao khi biết diện tích và 1 trong 2 đại lượng đó.
Ví dụ 1: Một hình trụ có bán kính đáy \(2cm\), chiều cao \(5cm\) thì có diện tích xung quanh là: \(S_{xq}=2\pi.2.5=20\pi\left(cm^2\right)\); diện tích toàn phần là: \(S_{tp}=2\pi.2.5+2\pi.2^2=28\pi\left(cm^2\right)\).
Ví dụ 2: Một hình trụ có chiều cao \(3cm\) và diện tích xung quanh \(18cm^2\). Khi đó chiều cao hình trụ là: \(h=\dfrac{S_{xq}}{2\pi r}=\dfrac{18\pi}{2\pi.3}=3\left(cm\right)\).
@60839@@60835@
4. Thể tích hình trụ
Ở lớp dưới ta đã biết:
Thể tích hình trụ tính bởi công thức:
\(V=\pi r^2h\)
trong đó \(r,h\) lần lượt là bán kính đáy và chiều cao hình trụ.
Ví dụ 1: Hình trụ có bán kính đáy \(2cm\), chiều cao \(3cm\) thì có thể tích là: \(V=\pi.2^2.3=12\pi\left(cm^3\right)\).
Ví dụ 2: Hình trụ có chiều cao \(5cm\), thể tích \(45\pi\left(cm^3\right)\). Khi đó, ta có: \(45\pi=\pi r^2.5\Rightarrow r^2=9\Rightarrow r=3\left(cm\right)\).
@60836@@60840@