Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
QL
Hướng dẫn giải
Thảo luận (1)
QL
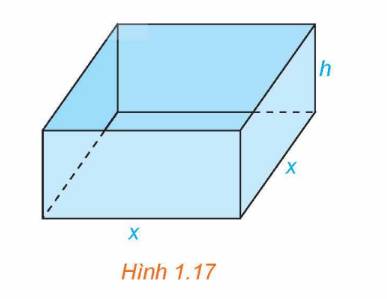
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng \(108c{m^2}\) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Hướng dẫn giải
Thảo luận (1)
Hình hộp trên có độ dài cạnh đáy là x (cm, \(x > 0\)) và chiều cao là h (cm, \(h > 0\))
Diện tích bề mặt của hình hộp là \(108c{m^2}\) nên \({x^2} + 4xh = 108 \Rightarrow h = \frac{{108 - {x^2}}}{{4x}}\left( {cm} \right)\)
Thể tích của hình hộp là: \(V = {x^2}.h = {x^2}.\frac{{108 - {x^2}}}{{4x}} = \frac{{108x - {x^3}}}{4}\left( {c{m^3}} \right)\)
Ta có: \(V' = \frac{{ - 3{x^2} + 108}}{4},V' = 0 \Leftrightarrow x = 6\) (do \(x > 0\))
Bảng biến thiên:
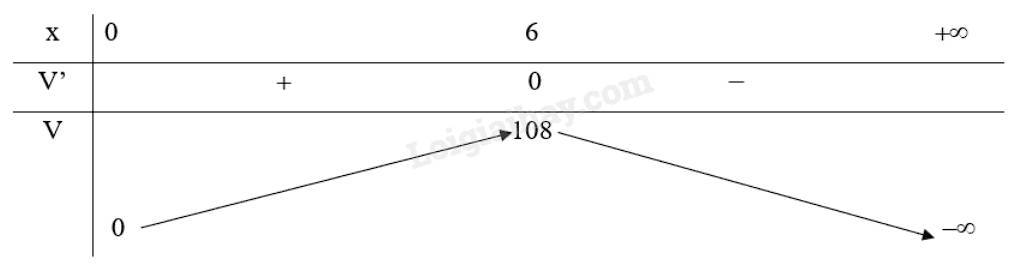
Do đó, thể tích của hình hộp là lớn nhất khi độ dài cạnh đáy \(x = 6\)cm
Khi đó, chiều cao của hình hộp là: \(\frac{{108 - {6^2}}}{{4.6}} = 3\left( {cm} \right)\).
Trả lời bởi Hà Quang Minh
QL
Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số Nleft( t right) - {t^3} + 12{t^2},0 le t le 12, trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).a) Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.b) Đạo hàm N’(t) biểu thị tốc độ lây lan của virus (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
Đọc tiếp
Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số \(N\left( t \right) = - {t^3} + 12{t^2},0 \le t \le 12,\) trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).
a) Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.
b) Đạo hàm N’(t) biểu thị tốc độ lây lan của virus (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
Hướng dẫn giải
Thảo luận (1)
a) Với \(0 \le t \le 12\) ta có:
\(N'\left( t \right) = - 3{t^2} + 24t,N'\left( t \right) = 0 \Leftrightarrow - 3{t^2} + 24t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\left( {tm} \right)\\t = 8\left( {tm} \right)\end{array} \right.\)
Ta có: \(N\left( 0 \right) = 0,N\left( 8 \right) = - {8^3} + {12.8^2} = 256,N\left( {12} \right) = - {12^3} + {12.12^2} = 0\)
Do đó, số người tối đa bị nhiễm bệnh ở địa phương là 256 người trong 12 tuần đầu.
b) Hàm số biểu thị tốc độ độ lây lan của virus là: \(N'\left( t \right) = - 3{t^2} + 24t\)
Đặt \(f\left( t \right) = - 3{t^2} + 24t\), với \(0 \le t \le 12\)
Ta có: \(f'\left( t \right) = - 6t + 24,f'\left( t \right) = 0 \Leftrightarrow t = 4\left( {tm} \right)\)
\(f\left( 0 \right) = 0,f\left( 4 \right) = - {3.4^2} + 24.4 = 48,f\left( {12} \right) = - {3.12^2} + 24.12 = - 144\)
Do đó, virus sẽ lây lan nhanh nhất khi \(t = 4\) (tuần thứ 4).
Trả lời bởi Hà Quang Minh
QL
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = 2{x^3} - 6x + 3\) trên đoạn \(\left[ { - 1;2} \right]\);
b) \(y = {x^4} - 3{x^2} + 2\) trên đoạn \(\left[ {0;3} \right]\);
c) \(y = x - \sin 2x\) trên đoạn \(\left[ {0;\pi } \right]\);
d) \(y = \left( {{x^2} - x} \right){e^x}\) trên đoạn \(\left[ {0;1} \right]\).
Hướng dẫn giải
Thảo luận (1)
a) Ta có: \(y' = 6{x^2} - 6,y' = 0 \Leftrightarrow 6{x^2} - 6 = 0 \Leftrightarrow x = \pm 1\) (thỏa mãn)
\(y\left( { - 1} \right) = 7,y\left( 1 \right) = - 1,y\left( 2 \right) = 7\)
Do đó, \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} y = y\left( 2 \right) = y\left( { - 1} \right) = 7,\mathop {\min }\limits_{\left[ { - 1;2} \right]} y = y\left( 1 \right) = - 1\)
b) Ta có: \(y' = 4{x^3} - 6x,y' = 0 \Leftrightarrow 4{x^3} - 6x = 0 \Leftrightarrow x = 0;x = \frac{{\sqrt 6 }}{2}\) (do \(x \in \left[ {0;3} \right]\))
\(y\left( 0 \right) = 2;y\left( {\frac{{\sqrt 6 }}{2}} \right) = \frac{{ - 1}}{4};y\left( 3 \right) = 56\)
Do đó, \(\mathop {\max }\limits_{\left[ {0;3} \right]} y = y\left( 3 \right) = 56,\mathop {\min }\limits_{\left[ {0;3} \right]} y = y\left( {\frac{{\sqrt 6 }}{2}} \right) = \frac{{ - 1}}{4}\)
c) Ta có: \(y' = 1 - 2\cos 2x,y' = 0 \Leftrightarrow 1 - 2\cos 2x = 0 \Leftrightarrow \cos 2x = \frac{1}{2} \Leftrightarrow x = \pm \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)\)
Mà \(x \in \left[ {0;\pi } \right] \Rightarrow x = \frac{\pi }{6};x = \frac{{5\pi }}{6}\)
\(y\left( 0 \right) = 0;y\left( {\frac{\pi }{6}} \right) = \frac{\pi }{6} - \frac{{\sqrt 3 }}{2};y\left( {\frac{{5\pi }}{6}} \right) = \frac{{5\pi }}{6} + \frac{{\sqrt 3 }}{2};y\left( \pi \right) = \pi \)
Do đó, \(\mathop {\max }\limits_{\left[ {0;\pi } \right]} y = y\left( {\frac{{5\pi }}{6}} \right) = \frac{{5\pi }}{6} + \frac{{\sqrt 3 }}{2},\mathop {\min }\limits_{\left[ {0;\pi } \right]} y = y\left( {\frac{\pi }{6}} \right) = \frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\)
d) \(y' = \left( {2x - 1} \right){e^x} + \left( {{x^2} - x} \right){e^x} = {e^x}\left( {{x^2} + x - 1} \right)\)
\(y' = 0 \Leftrightarrow {e^x}\left( {{x^2} + x - 1} \right) = 0 \Leftrightarrow x = \frac{{ - 1 + \sqrt 5 }}{2}\) (do \(x \in \left[ {0;1} \right]\))
\(y\left( 0 \right) = 0;y\left( {\frac{{ - 1 + \sqrt 5 }}{2}} \right) = \left( {2 - \sqrt 5 } \right){e^{\frac{{ - 1 + \sqrt 5 }}{2}}};y\left( 1 \right) = 0\)
Do đó, \(\mathop {\max }\limits_{\left[ {0;1} \right]} y = y\left( 0 \right) = y\left( 1 \right) = 0,\mathop {\min }\limits_{\left[ {0;1} \right]} y = y\left( {\frac{{ - 1 + \sqrt 5 }}{2}} \right) = \left( {2 - \sqrt 5 } \right){e^{\frac{{ - 1 + \sqrt 5 }}{2}}}\)
Trả lời bởi Hà Quang Minh
QL
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = - {x^2} + 4x + 3\);
b) \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\);
c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) trên \(\left( {1; + \infty } \right)\);
d) \(y = \sqrt {4x - 2{x^2}} \).
Hướng dẫn giải
Thảo luận (1)
a) Ta có: \(y = - {x^2} + 4x + 3 = - {\left( {x - 2} \right)^2} + 7 \le 7\) với mọi số thực x.
Dấu “=” xảy ra khi \(x - 2 = 0 \Leftrightarrow x = 2\).
Do đó, \(\max f\left( x \right) = f\left( 2 \right) = 7\), hàm số không có giá trị nhỏ nhất.
b) GTLN, GTNN của \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\)
Ta có: \(y' = 3{x^2} - 4x,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\left( {tm} \right)\\x = \frac{4}{3}\left( {tm} \right)\end{array} \right.\)
Bảng biến thiên:
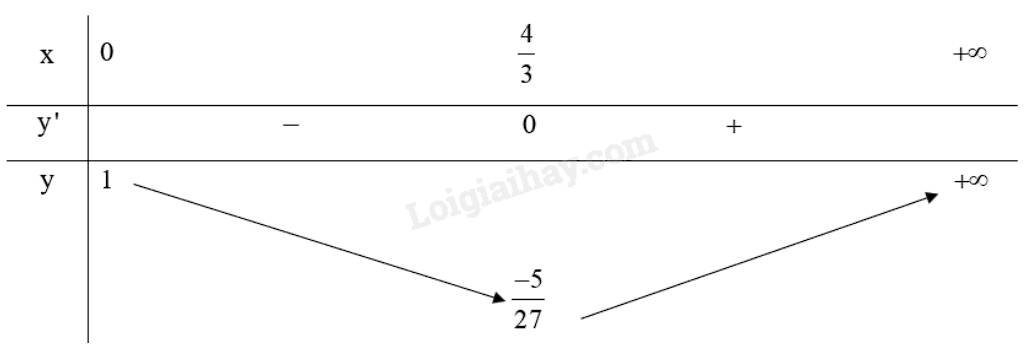
Do đó, \(\mathop {\min }\limits_{\left[ {0; + \infty } \right)} y = y\left( {\frac{4}{3}} \right) = \frac{{ - 5}}{{27}}\), hàm số không có giá trị lớn nhất.
c) Ta có: \(y' = \frac{{\left( {2x - 2} \right)\left( {x - 1} \right) - \left( {{x^2} - 2x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}}\)
\(y' = 0 \Leftrightarrow x = 1 + \sqrt 2 \) (do \(x \in \left( {1; + \infty } \right)\))
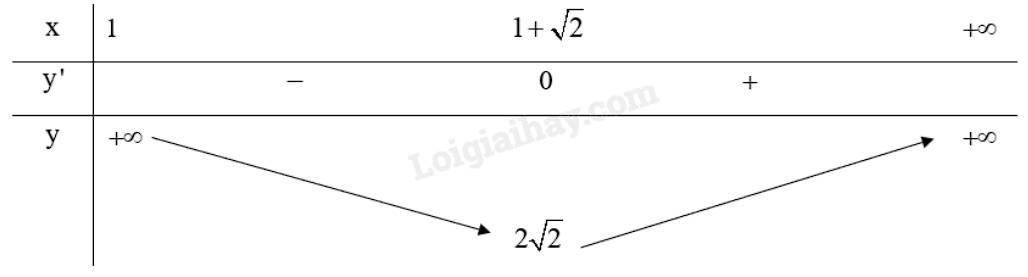
Do đó, \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = y\left( {1 + \sqrt 2 } \right) = 2\sqrt 2 \), hàm số không có giá trị lớn nhất trên \(\left( {1; + \infty } \right)\).
d) Tập xác định của hàm số là: \(D = \left[ {0;2} \right]\)
\(y' = \frac{{\left( {4x - 2{x^2}} \right)'}}{{2\sqrt {4x - 2{x^2}} }} = \frac{{4 - 4x}}{{2\sqrt {4x - 2{x^2}} }} = \frac{{2\left( {1 - x} \right)}}{{\sqrt {4x - 2{x^2}} }}\)
\(y' = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
\(y\left( 0 \right) = 0;y\left( 1 \right) = \sqrt 2 ;y\left( 2 \right) = 0\)
Do đó, \(\mathop {\max }\limits_{\left[ {0;2} \right]} y = y\left( 1 \right) = \sqrt 2 ,\mathop {\min }\limits_{\left[ {0;2} \right]} y = y\left( 0 \right) = y\left( 2 \right) = 0\)
Trả lời bởi Hà Quang Minh
QL
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) \(y = 2{x^3} - 3{x^2} + 5x + 2\) trên đoạn \(\left[ {0;2} \right]\);
b) \(y = \left( {x + 1} \right){e^{ - x}}\) trên đoạn \(\left[ { - 1;1} \right]\).
Hướng dẫn giải
Thảo luận (1)
a) Ta có: \(y' = 6{x^2} - 6x + 5 = 6\left( {{x^2} - x + \frac{5}{6}} \right) = 6{\left( {x - \frac{1}{2}} \right)^2} + \frac{7}{2} > 0\;\forall x \in \left[ {0;2} \right]\)
Do đó, hàm số \(y = 2{x^3} - 3{x^2} + 5x + 2\) đồng biến trên \(\left[ {0;2} \right]\).
Ta có: \(y\left( 0 \right) = 2;y\left( 2 \right) = {2.2^3} - {3.2^2} + 5.2 + 2 = 16\)
Do đó, \(\mathop {\max }\limits_{\left[ {0;2} \right]} y = y\left( 2 \right) = 16,\mathop {\min }\limits_{\left[ {0;2} \right]} y = y\left( 0 \right) = 2\)
b) Ta có: \(y' = {e^{ - x}} - \left( {x + 1} \right){e^{ - x}} = {e^{ - x}}\left( {1 - x - 1} \right) = - x.{e^{ - x}}\)
\(y' = 0 \Leftrightarrow - x.{e^{ - x}} = 0 \Leftrightarrow x = 0\) (thỏa mãn \(x \in \left[ { - 1;1} \right]\))
\(y\left( { - 1} \right) = 0;y\left( 0 \right) = 1;y\left( 1 \right) = \frac{2}{e}\)
Do đó, \(\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = y\left( 0 \right) = 1,\mathop {\min }\limits_{\left[ { - 1;1} \right]} y = y\left( { - 1} \right) = 0\)
Trả lời bởi Hà Quang Minh
QL
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = \sqrt {2x - {x^2}} \);
b) \(y = - x + \frac{1}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\).
Hướng dẫn giải
Thảo luận (1)
a) Tập xác định của hàm số là \(\left[ {0;2} \right]\).
Với \(x \in \left[ {0;2} \right]\) ta có: \(y' = \frac{{\left( {2x - {x^2}} \right)'}}{{2\sqrt {2x - {x^2}} }} = \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }}\), \(y' = 0 \Leftrightarrow \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }} = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
Lập bảng biến thiên của hàm số trên đoạn \(\left[ {0;2} \right]\):
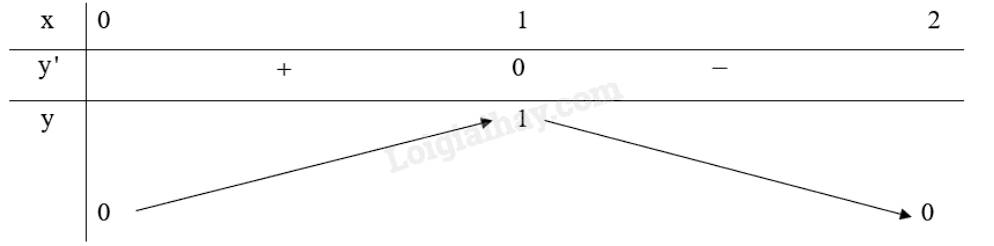
Từ bảng biến thiên ta thấy: \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 0,\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 1 \right) = 1\).
b) Với \(x \in \left( {1; + \infty } \right)\) ta có:
Ta có: \(y' = - 1 + \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\;\forall x \in \left( {1; + \infty } \right)\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( { - x + \frac{1}{{x - 1}}} \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - x + \frac{1}{{x - 1}}} \right) = - \infty \)
Lập bảng biến thiên của hàm số trên \(\left( {1; + \infty } \right)\):
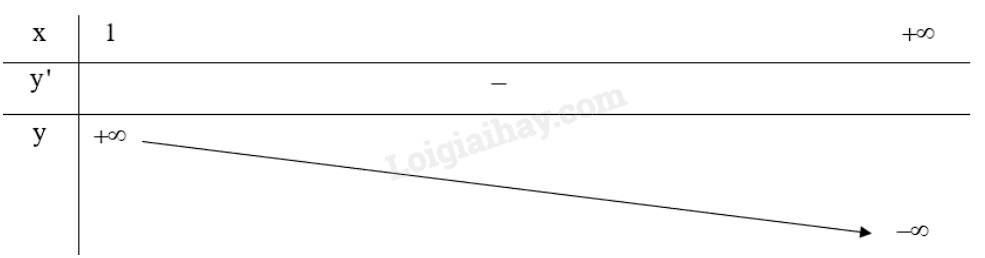
Vậy hàm số không có giá trị lớn nhất, giá trị nhỏ nhất trên \(\left( {1; + \infty } \right)\).
Trả lời bởi Hà Quang Minh
QL
Cho hàm số y fleft( x right) {x^2} - 2x với x in left[ {0;3} right], có đồ thị như Hình 1.15.a) Giá trị lớn nhất M của hàm số trên đoạn left[ {0;3} right] là bao nhiêu? Tìm {x_0} sao cho fleft( {{x_0}} right) M.b) Giá trị nhỏ nhất m của hàm số trên đoạn left[ {0;3} right] là bao nhiêu? Tìm {x_0} sao cho fleft( {{x_0}} right) m.
Đọc tiếp
Cho hàm số \(y = f\left( x \right) = {x^2} - 2x\) với \(x \in \left[ {0;3} \right]\), có đồ thị như Hình 1.15.
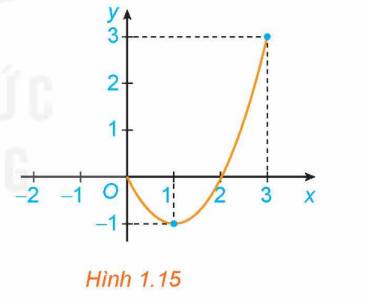
a) Giá trị lớn nhất M của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = M\).
b) Giá trị nhỏ nhất m của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = m\).
Hướng dẫn giải
Thảo luận (1)
a) Giá trị lớn nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(M = 3\).
Với \({x_0} = 3\) thì \(f\left( 3 \right) = 3\).
b) Giá trị nhỏ nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(m = - 1\).
Với \({x_0} = 1\) thì \(f\left( 1 \right) = - 1\).
Trả lời bởi Hà Quang Minh
QL
Xét hàm số y fleft( x right) {x^3} - 2{x^2} + 1 trên đoạn left[ { - 1;2} right], với đồ thị như Hình 1.16.a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn left[ { - 1;2} right].b) Tính đạo hàm f’(x) và tìm các điểm x in left( { - 1;2} right) mà fleft( x right) 0.c) Tính giá trị của hàm số tại hai đầu mút của đoạn left[ { - 1;2} right] và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với mathop {min }limits_{left[ { - 1;2} right]} fleft( x right), số...
Đọc tiếp
Xét hàm số \(y = f\left( x \right) = {x^3} - 2{x^2} + 1\) trên đoạn \(\left[ { - 1;2} \right]\), với đồ thị như Hình 1.16.
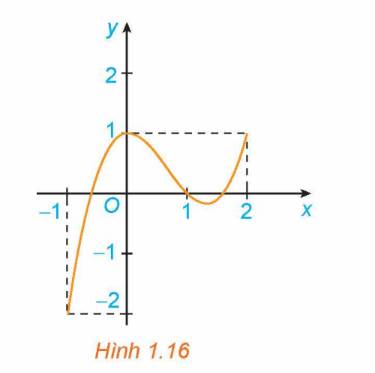
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;2} \right]\).
b) Tính đạo hàm f’(x) và tìm các điểm \(x \in \left( { - 1;2} \right)\) mà \(f'\left( x \right) = 0\).
c) Tính giá trị của hàm số tại hai đầu mút của đoạn \(\left[ { - 1;2} \right]\) và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right)\), số lớn nhất trong các giá trị này với \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right)\).
Hướng dẫn giải
Thảo luận (1)
a) Nhìn vào đồ thị ta thấy, trên đoạn \(\left[ { - 1;2} \right]\) ta có:
+ Giá trị lớn nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 1\).
+ Giá trị nhỏ nhất của hàm số là \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( { - 1} \right) = - 2\).
b) \(f'\left( x \right) = 3{x^2} - 4x,f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{4}{3}\end{array} \right.\)
Vậy \(x = 0,x = \frac{4}{3}\) thì \(f'\left( x \right) = 0\).
c) Ta có: \(f\left( 0 \right) = 1;f\left( {\frac{4}{3}} \right) = {\left( {\frac{4}{3}} \right)^3} - 2.{\left( {\frac{4}{3}} \right)^2} + 1 = \frac{{ - 5}}{{27}};f\left( { - 1} \right) = {\left( { - 1} \right)^3} - 2.{\left( { - 1} \right)^2} + 1 = - 2\);
\(f\left( 2 \right) = {2^3} - {2.2^2} + 1 = 1\)
Do đó, số nhỏ nhất trong các giá trị này là \( - 2\), số lớn nhất trong các giá trị này là 1.
Ta thấy: \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = 1\), \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = - 2\).
Trả lời bởi Hà Quang Minh
QL
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) \(y = {x^4} - 2{x^2} + 3\);
b) \(y = x.{e^{ - x}}\);
c) \(y = x\ln x\);
d) \(y = \sqrt {x - 1} + \sqrt {3 - x} \).
Hướng dẫn giải
Thảo luận (1)
a) \(y = {x^4} - 2{x^2} + 3\)
\(y' = 4{x^3} - 4x,y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\)
\(y\left( 0 \right) = 3;y\left( 1 \right) = y\left( { - 1} \right) = 2\)
Do đó, \(\mathop {\max }\limits_{\left( { - \infty ; + \infty } \right)} y = y\left( 0 \right) = 3,\mathop {\min }\limits_{\left( { - \infty ; + \infty } \right)} y = y\left( 1 \right) = y\left( { - 1} \right) = 2\)
b) Ta có: \(y' = {e^{ - x}} - x.{e^{ - x}},y' = 0 \Leftrightarrow {e^{ - x}} - x.{e^{ - x}} = 0 \Leftrightarrow {e^{ - x}}\left( {1 - x} \right) = 0 \Leftrightarrow x = 1\)
Bảng biến thiên:
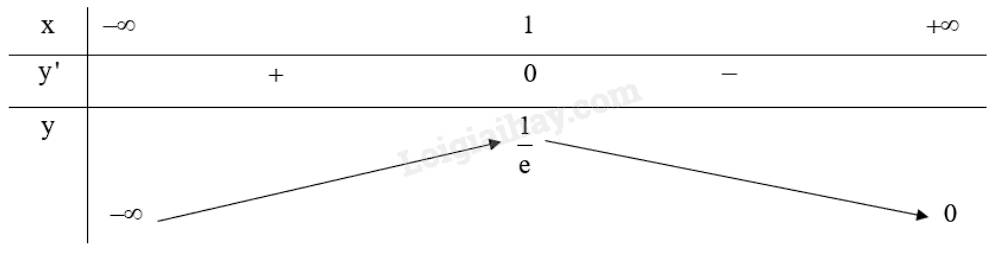
Do đó, \(\mathop {\max }\limits_{\left( { - \infty ; + \infty } \right)} y = y\left( 1 \right) = \frac{1}{e}\), hàm số không có giá trị nhỏ nhất.
c) Tập xác định của hàm số là: \(D = \left( {0; + \infty } \right)\)
\(y' = \ln x + x.\frac{1}{x} = \ln x + 1,y' = 0 \Leftrightarrow \ln x + 1 = 0 \Leftrightarrow x = \frac{1}{e}\) (thỏa mãn)
Bảng biến thiên:
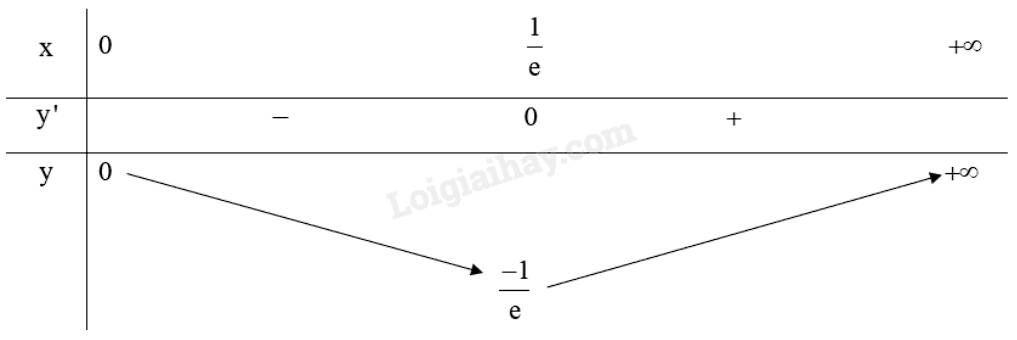
Hàm số không có giá trị lớn nhất, \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} y = y\left( {\frac{1}{e}} \right) = \frac{{ - 1}}{e}\)
d) Tập xác định của hàm số là \(\left[ {1;3} \right]\).
\(y' = \frac{1}{{2\sqrt {x - 1} }} - \frac{1}{{2\sqrt {3 - x} }},y' = 0 \Leftrightarrow \frac{1}{{2\sqrt {x - 1} }} - \frac{1}{{2\sqrt {3 - x} }} = 0 \Leftrightarrow \frac{{\sqrt {3 - x} - \sqrt {x - 1} }}{{2\sqrt {3 - x} \sqrt {x - 1} }} = 0\)
\( \Leftrightarrow \sqrt {3 - x} = \sqrt {x - 1} \Leftrightarrow 3 - x = x - 1 \Leftrightarrow x = 2\left( {tm} \right)\)
\(y\left( 1 \right) = \sqrt 2 ;y\left( 2 \right) = 2;y\left( 3 \right) = \sqrt 2 \)
Do đó, \(\mathop {\max }\limits_{\left[ {1;3} \right]} y = y\left( 2 \right) = 2,\mathop {\min }\limits_{\left[ {1;3} \right]} y = y\left( 1 \right) = y\left( 3 \right) = \sqrt 2 \)
Trả lời bởi Hà Quang Minh
Gọi chiều dài của hình chữ nhật là x (cm, \(0 < x < 12\))
Chiều rộng của hình chữ nhật là \(12 - x\left( {cm} \right)\)
Diện tích của hình chữ nhật là: \(x\left( {12 - x} \right) = - {x^2} + 12x\;\left( {c{m^2}} \right)\)
Đặt \(S\left( x \right) = - {x^2} + 12x,x \in \left( {0;12} \right)\)
\(S'\left( x \right) = - 2x + 12,S'\left( x \right) = 0 \Leftrightarrow x = 6\left( {tm} \right)\)
Bảng biến thiên:
Do đó, trong các hình có cùng chu vi thì hình chữ nhật có diện tích lớn nhất là \(36c{m^2}\).
Trả lời bởi Hà Quang Minh