a) Tập xác định của hàm số là \(\left[ {0;2} \right]\).
Với \(x \in \left[ {0;2} \right]\) ta có: \(y' = \frac{{\left( {2x - {x^2}} \right)'}}{{2\sqrt {2x - {x^2}} }} = \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }}\), \(y' = 0 \Leftrightarrow \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }} = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
Lập bảng biến thiên của hàm số trên đoạn \(\left[ {0;2} \right]\):
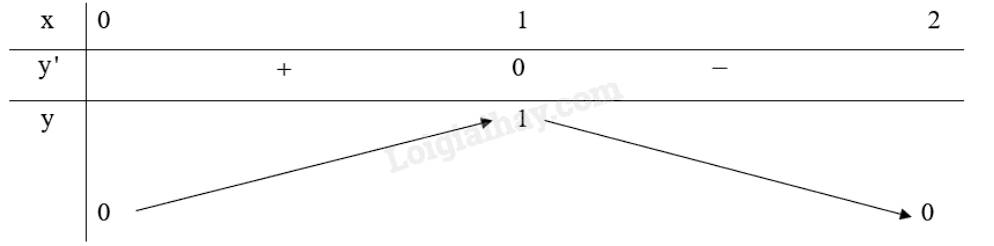
Từ bảng biến thiên ta thấy: \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 0,\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 1 \right) = 1\).
b) Với \(x \in \left( {1; + \infty } \right)\) ta có:
Ta có: \(y' = - 1 + \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\;\forall x \in \left( {1; + \infty } \right)\)
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( { - x + \frac{1}{{x - 1}}} \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - x + \frac{1}{{x - 1}}} \right) = - \infty \)
Lập bảng biến thiên của hàm số trên \(\left( {1; + \infty } \right)\):
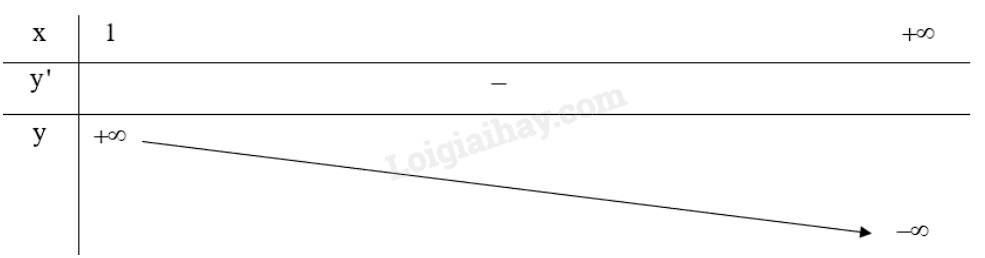
Vậy hàm số không có giá trị lớn nhất, giá trị nhỏ nhất trên \(\left( {1; + \infty } \right)\).
