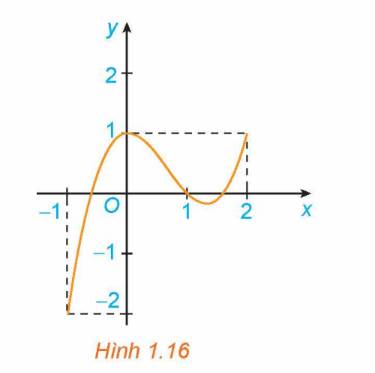
Xét hàm số \(y = f\left( x \right) = {x^3} - 2{x^2} + 1\) trên đoạn \(\left[ { - 1;2} \right]\), với đồ thị như Hình 1.16.
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;2} \right]\).
b) Tính đạo hàm f’(x) và tìm các điểm \(x \in \left( { - 1;2} \right)\) mà \(f'\left( x \right) = 0\).
c) Tính giá trị của hàm số tại hai đầu mút của đoạn \(\left[ { - 1;2} \right]\) và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right)\), số lớn nhất trong các giá trị này với \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right)\).
a) Nhìn vào đồ thị ta thấy, trên đoạn \(\left[ { - 1;2} \right]\) ta có:
+ Giá trị lớn nhất của hàm số là \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 1\).
+ Giá trị nhỏ nhất của hàm số là \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( { - 1} \right) = - 2\).
b) \(f'\left( x \right) = 3{x^2} - 4x,f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{4}{3}\end{array} \right.\)
Vậy \(x = 0,x = \frac{4}{3}\) thì \(f'\left( x \right) = 0\).
c) Ta có: \(f\left( 0 \right) = 1;f\left( {\frac{4}{3}} \right) = {\left( {\frac{4}{3}} \right)^3} - 2.{\left( {\frac{4}{3}} \right)^2} + 1 = \frac{{ - 5}}{{27}};f\left( { - 1} \right) = {\left( { - 1} \right)^3} - 2.{\left( { - 1} \right)^2} + 1 = - 2\);
\(f\left( 2 \right) = {2^3} - {2.2^2} + 1 = 1\)
Do đó, số nhỏ nhất trong các giá trị này là \( - 2\), số lớn nhất trong các giá trị này là 1.
Ta thấy: \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = 1\), \(\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = - 2\).
