Cho hàm số \(y = f\left( x \right) = {x^2} - 2x\) với \(x \in \left[ {0;3} \right]\), có đồ thị như Hình 1.15.
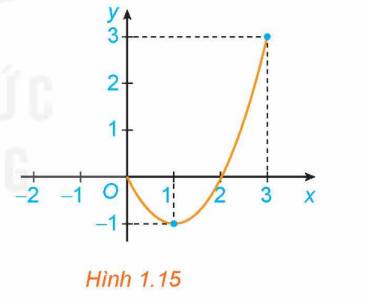
a) Giá trị lớn nhất M của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = M\).
b) Giá trị nhỏ nhất m của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = m\).
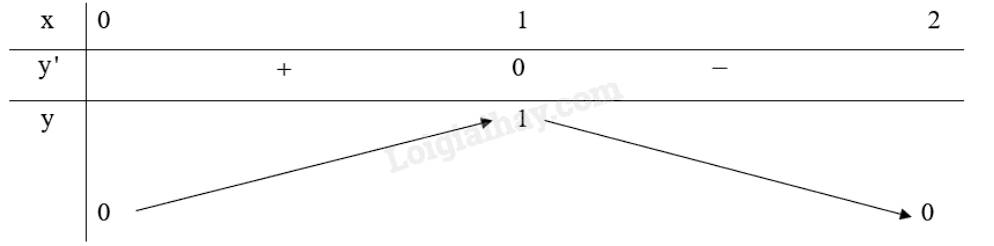
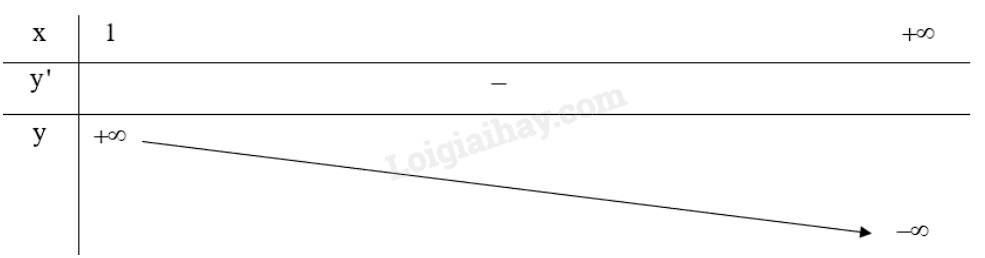
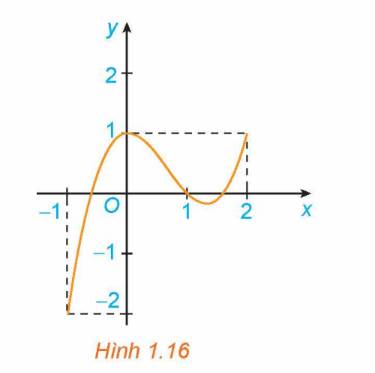
a) Giá trị lớn nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(M = 3\).
Với \({x_0} = 3\) thì \(f\left( 3 \right) = 3\).
b) Giá trị nhỏ nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(m = - 1\).
Với \({x_0} = 1\) thì \(f\left( 1 \right) = - 1\).
Trả lời bởi Hà Quang Minh