Bài 1: Dao động điều hoà

Tham khảo:

Dao động là chuyển động mà vật chuyển động qua lại quanh một vị trí đặc biệt gọi là vị trí cân bằng.

- Tần số góc: `\omega` `(rad//s)`

- Tần số: `f (Hz)`

`->` Mối liên hệ giữa tần số góc và tần số trong dao động điều hòa là:

                  `\omega = 2\pi.f`

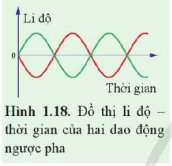
Hai dao động đều có chu kì `T` và thời điểm `t=0` tại vị trí cân bằng, nhưng tại cùng thời điểm tiếp theo thì:

- Dao động màu xanh đến biên dương.

- Dao động màu hồng đến biên âm.

  Mà từ biên dương đến biên âm chênh lệch 1 góc `\pi`.

`=>` Độ lệch pha của hai dao động là: `\pi (rad)`

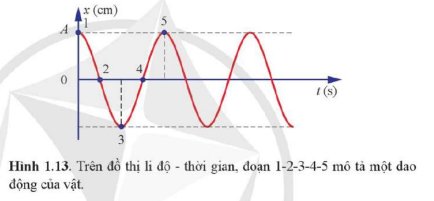
Li độ \(x=Acos\left(\omega t+\varphi\right)\)

Tại thời điểm t = 0, li độ x = A sau đó li độ giảm dần, vật chuyển động theo chiều âm. Do đó, pha ban đầu của dao động là \(\varphi=0\)

Vật chuyển động trong thời gian \(\dfrac{T}{2}\) đến vị trí thứ 3, thực hiện nửa dao động tương ứng với góc \(\pi\) rad.

Pha của dao động tại vị trí thứ 3 là \(\omega t+\varphi=\pi\) (rad)

Vật chuyển động trong thời gian \(\dfrac{3T}{4}\) đến vị trí thứ 3, thực hiện \(\dfrac{3}{4}\) dao động tương ứng với góc \(\dfrac{3\pi}{2}\) rad

Pha của dao động tại vị trí thứ 4 là \(\omega t+\varphi=\dfrac{3\pi}{2}\) (rad)

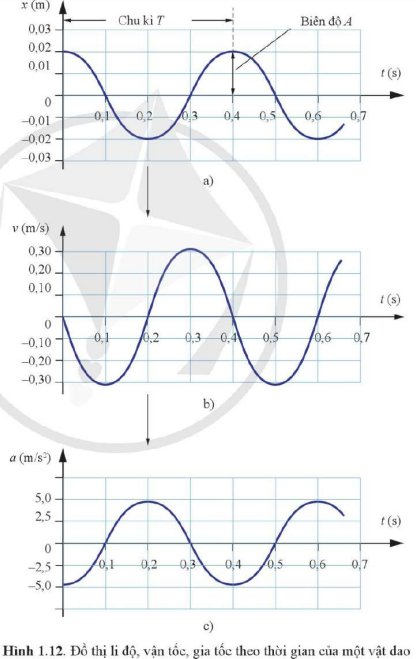
`***` Hình `a`:

     `a, \omega =[2\pi]/[0,4]=5\pi (rad//s)`

     `b, A=0,03(m)=3(cm)`

     `c, v_[max]=5\pi .3=15 \pi(cm//s)`

     `d, a_[max]=(5\pi)^2 .3=75 \pi^2 (cm//s^2)`

`***` Hình `b`:

    `a, \omega =[2\pi]/[0,4]= 5 \pi(rad//s)`

    `b, A=[0,3]/[5\pi]=3/[50 \pi] (m)=6/[\pi] (cm)`

    `c, v_[max]=30 (cm//s)`

    `d, a_[max]=30.5\pi=150\pi (cm//s^2)`

`***` Hình `c`:

    `a, \omega=[2\pi]/[0,4]=5\pi (rad//s)`

    `b, A=5/[(5\pi)^2]=1/[5\pi^2] (m)`

    `c, v_[max]=5\pi . 1/[5\pi^2]=1/[\pi] (m//s)`

    `d, a_[max]=5(m//s^2)`

Pha dao động của phương trình là: `10 \pi t + \varphi/2`

   `=>` Pha dao động tại thời điểm `1/30 s` là: `10\pi .1/30 + \varphi/2=\pi/3+ \varphi/2`.

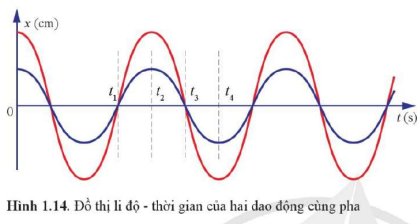
- Tại thời điểm `t_3` thì `2` vật đều đang ở vị trí cân bằng và chuyển động theo chiều dương.

- Tại thời điểm `t_4` thì `2` vật đều ở biên âm.

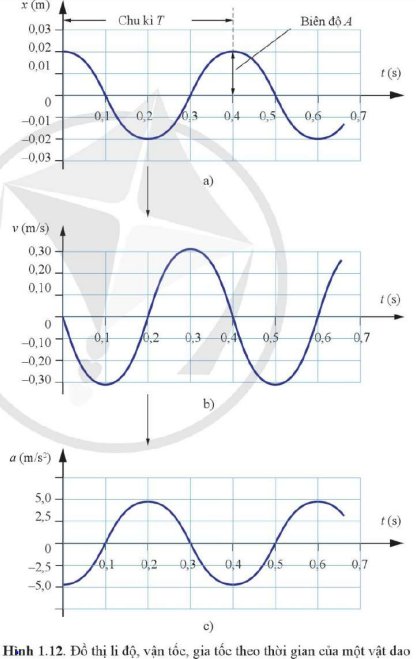
Dựa vào các đồ thị ở Hình `1.12` ta có:

- Các thời điểm gia tốc của xe bằng `0` là `t={0,1 ; 0,3 ; 0,5} (s)`

- Các thời điểm gia tốc của xe cực đại là `t={0 ; 0,2 ; 0,4 ; 0,6} (s)`

Cách làm: dựa vào đồ thị ở hình `c`, ta chiếu các thời điểm ứng với trục `t` sang trục `a`.

Xây dựng phương án: Treo quả cầu ở một đầu lò xo, đầu còn lại của lò xo treo lên giá thí nghiệm. Nối một sợi dây với quả cầu. Ban đầu, vật treo trên lò xo đứng yên, lò xo nằm trên trục thẳng đứng. Ta tác dụng một lực kéo nhỏ lên sợi dây theo phương thẳng đứng chiều từ trên xuống dưới.

Thực hiện phương án: Quan sát thấy lò xo dãn rồi co lần lượt, vật chuyển động qua lại quanh vị trí ban đầu (vị trí cân bằng). Như vậy, ta có được dao động của vật treo ở đầu lò xo.

-Tham khảo-

Một số dao động quan sát được trong thực tế:

- Dây đàn ghita dao động sau khi gảy.

- Màng trống dao động sau khi gõ vào. 

- Con lắc đồng hồ dao động.

- Âm thoa dao động sau khi gõ vào

- Huyền dao động (nhấp nhô lên xuống tại chỗ) trên mặt nước.

....v.v....