Bài 1: Dao động điều hoà

I. Dao động

1. Thí nghiệm tạo dao động

Thực hiện thí nghiệm sau:

Dụng cụ: Một quả cầu kim loại nhỏ, sợi dây mảnh nhẹ, giá thí nghiệm.

Tiến hành: Treo quả cầu vào giá thí nghiệm. Khi quả cầu đứng yên tại vị trí cân bằng, dây treo có phương thẳng đứng. Kéo quả cầu khỏi vị trí cân bằng một đoạn nhỏ rồi buông tay cho quả cầu chuyển động. 

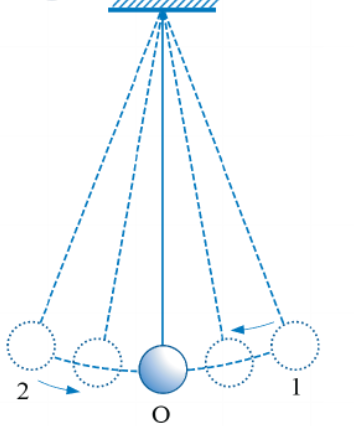
Kết quả: Quả cầu chuyển động qua lại quanh vị trí cân bằng. Nếu thả quả cầu ở vị trí 1 thì quả cầu sẽ đi sang trái qua O đến vị trí 2 thì dừng rồi đi ngược lại. Chuyển động được lặp lại liên tiếp như vậy nếu không có lực cản

Chuyển động qua lại quanh một ví trí cân bằng được gọi là dao động.

Ví dụ: Nêu một số ví dụ về dao động trong cuộc sống.

Giải: 

Một số chuyển động là dao động trong cuộc sống là: chuyển động của chiếc thuyền nhấp nhô tại chỗ neo, rung động của dây đàn ghita, chuyển động của chiếc lá quanh vị trí khi lặng gió, chuyển động của con lắc đồng hồ,....

2. Dao động tự do

Trong ví dụ ở phần 1, nếu không có lực cản thì chuyển động của quả cầu cứ tiếp diễn, không dừng lại, dao động của quả cầu là dao động tự do. Các vật trong điều kiện trong có lực cản, các vật này đều dao động tự do sau khi chịu một tác động ban đầu làm nó dao động.

Trong các tình huống thực tế, lực cản làm cho năng lượng dao động của vật bị giảm dần và năng lượng này chuyển hóa thành năng lượng nhiệt. Các dao động này sẽ bị tắt dần. Sau một khoảng thời gian, vật sẽ ngừng dao động.

3. Biên độ, chu kỳ, tần số của dao động

Độ dịch chuyển của vật so với vị trí cân bằng gọi là li độ.

Độ dịch chuyển lớn nhất của vật dao động so với vị trí cân bằng được gọi là biên độ của dao động. Kí hiệu: A. Biên độ của dao động là một số dương.

Khoảng thời gian để vật thực hiện một dao động được gọi là chu kì của dao động. Kí hiệu: T. Đơn vị của chu kì là giây (s).

Số dao động vật thực hiện được trong một giây gọi là tần số của dao động. Kí hiệu là f. Đơn vị của tần số là hertz (Hz).

1 Hz là một dao động trong một giây.

Ví dụ: Xác định biên độ, chu kì và tần số của dao động có đồ thị li độ - thời gian được biểu diễn ở hình dưới đây:

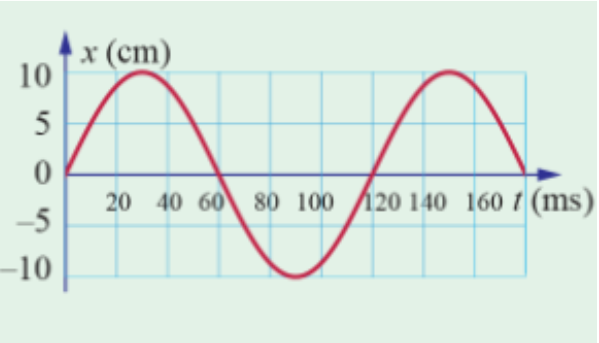
Giải:

Ta nhận thấy đồ thị đi lên điểm cao nhất ứng với li độ x = 10 (cm) và điểm thấp nhất ứng với li độ x = - 10 (cm). Như vậy, biên độ của dao động là A = |10| = |-10| = 10 (cm).

Từ vị trí t = 0 (ms) đến t = 120 (ms) vật hoàn thành một chu kỳ dao động (quay trở lại vị trí cũ với hướng chuyển động cũ). Vậy chu kì của dao động là T = 120 - 0 = 120 (ms).

Vật hoàn thành 1 chu kỳ trong 120 ms = 0,12 s, vậy tần số tức số dao động vật thực hiện được trong 1 giây là: \(f=\dfrac{1}{0,12}=\dfrac{25}{3}\left(Hz\right)\)

​

II. Dao động điều hòa

1. Định nghĩa

Dao động điều hòa là dao động trong đó li độ của vật là một hàm côsin (hoặc sin) của thời gian.

Phương trình dao động điều hòa: \(x=Acos\left(\omega t+\varphi\right)\)

Trong đó  \(A,\omega,\varphi\) là các hằng số. 

Dao động điều hòa cũng có các đại lượng biên độ A, chu kì T, tần số f như dao động nói chung.

2. Tần số góc

Công thức: \(\omega=\dfrac{2\pi}{T}=2\pi.f\)

Đại lượng \(\omega\) là tần số góc của dao động và có đơn vị là radian trên giây (rad/s).

3. Vận tốc và gia tốc trong dao động điều hòa

Công thức: \(v=-\omega Asin\left(\omega t+\varphi\right)\)

và \(a=-\omega^2Acos\left(\omega t+\varphi\right)\)

Vận tốc và gia tốc của vật dao động điều hòa cũng biến thiên tuần hoàn theo quy luật hàm số sin (côsin)  cùng chu kì T của li độ.

Mối liên hệ giữa gia tốc và li độ của vật dao động điều hòa là:

\(a=-\omega^2x\)

4. Pha của dao động và độ lệch pha

Pha của dao động

Pha của dao động tại một thời điểm được tính bằng số phần đã thực hiện của một chu kì kể từ khi bắt đầu chu kì đó. Đơn vị: rad.

Trong phương trình dao động điều hòa, đại lượng \(\left(\omega t+\varphi\right)\) là pha của dao động điều hòa tại thời điểm t.

Tại thời điểm t = 0, pha của dao động là \(\varphi\) nên \(\varphi\) được gọi là pha ban đầu của dao động.

Dao động cùng pha

Tại mỗi thời điểm, hai vật dao động đều có trạng thái giống nhau thì dao động cùng pha với nhau.

Dao động lệch pha

Tại thời điểm bất kỳ, vật này đạt li độ cực đại sớm hơn vật kia một khoảng thời gian \(\Delta t\) thì hai vật dao động lệch pha. Độ lệch pha của hai vật không đổi khi chúng dao động, luôn ứng với một phần của chu kì, tức là bằng \(\text{​​}\text{​​}\dfrac{\Delta t}{T}\).

Độ lệch pha giữa hai dao động có thể được đo bằng số phần của chu kì dao động hoặc bằng đơn vị độ hay radian. Trong thực tế, độ lệch pha được đo bằng đơn vị là radian.