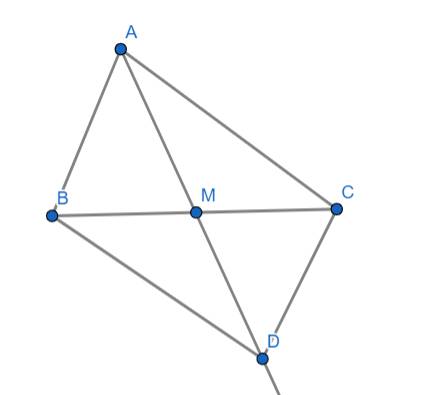
a) Xét ΔAMB và ΔDMC có:
\(AM=CM\) (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(BM=CM\) (M là trung điểm của BC)
\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)
b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow AB=DC\) (2 cạnh t.ứng)
c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)

