Question

Xác định tọa độ giao điểm của (P):y=\(\dfrac{2}{3}x^2\) và (d):y=x+3 bằng  phương pháp đại số và đồ thị

Answer 1

*Phương pháp đại số

Phương trình hoành độ giao điểm là:

\(\dfrac{2}{3}x^2=x+3\)

=>\(\dfrac{2}{3}x^2-x-3=0\)

=>\(2x^2-3x-9=0\)

=>(x-3)(2x+3)=0

=>\(\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{2}\end{matrix}\right.\)

Thay x=3 vào y=x+3, ta được:

y=3+3=6

Thay x=-3/2 vào y=x+3, ta được:

\(y=-\dfrac{3}{2}+3=\dfrac{3}{2}\)

vậy: (P) cắt (d) tại A(3;6); B(-3/2;3/2)

*Phương pháp đồ thị:

 

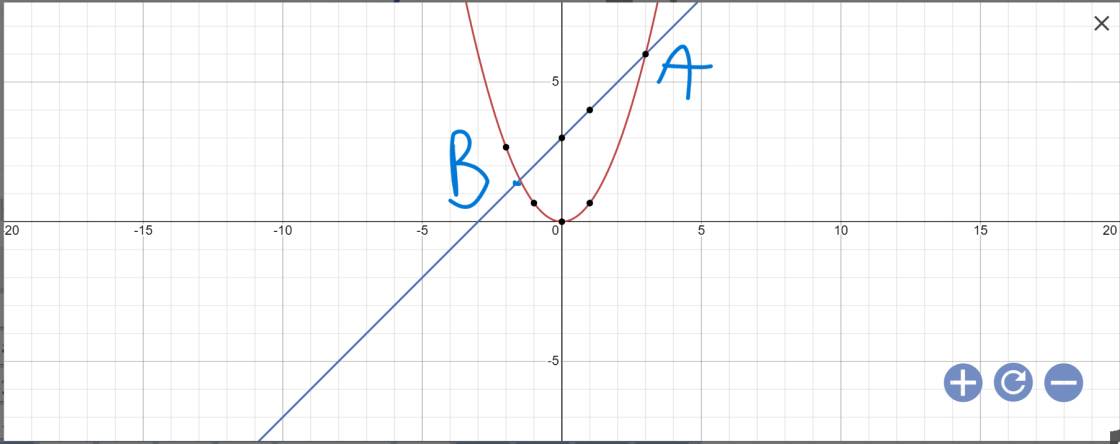
qua đồ thị, ta có thể thấy (P) cắt (d) tại A(3;6); B(-3/2;3/2)