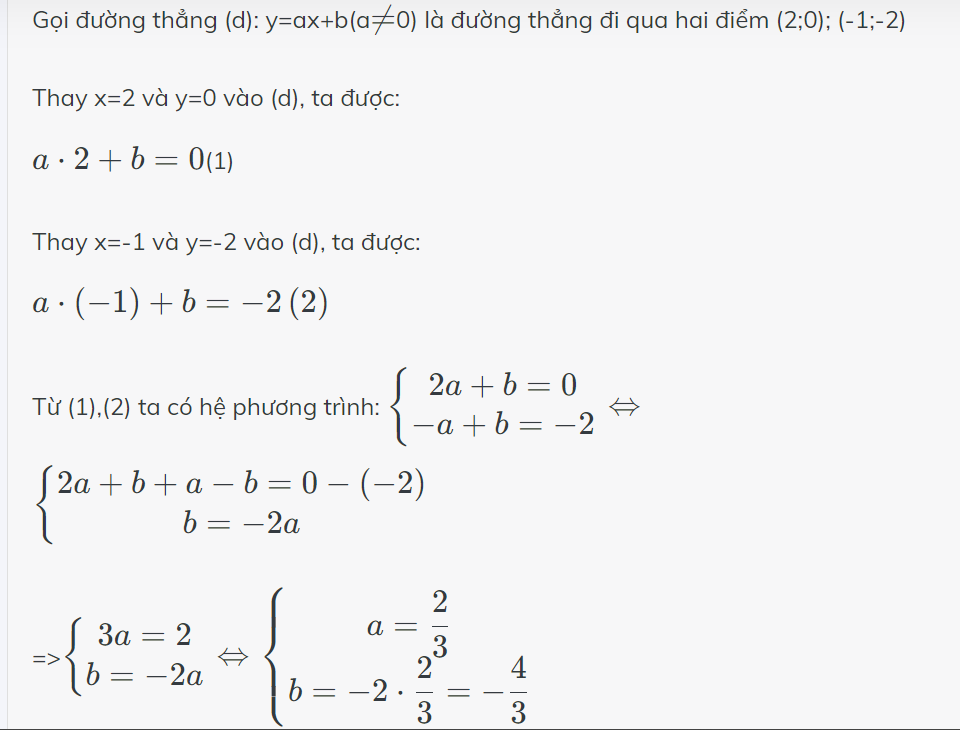
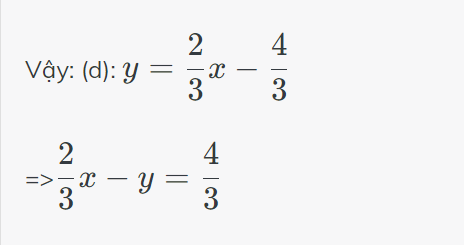
Vậy: Phương trình bậc nhất hai ẩn cần tìm là \(\dfrac{2}{3}x-y=\dfrac{4}{3}\)
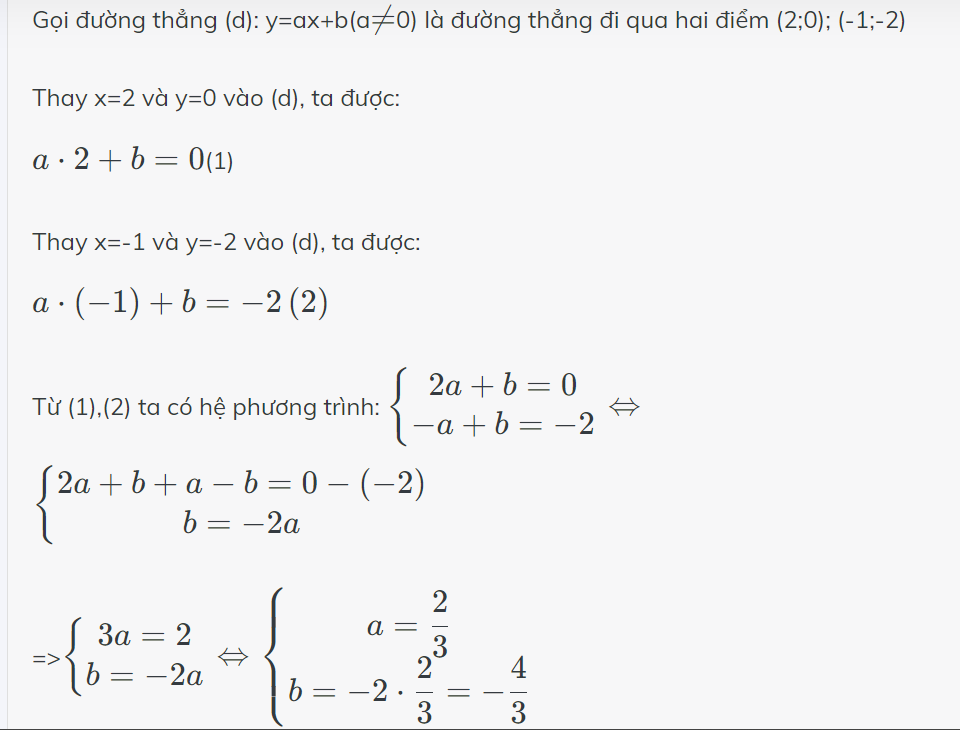
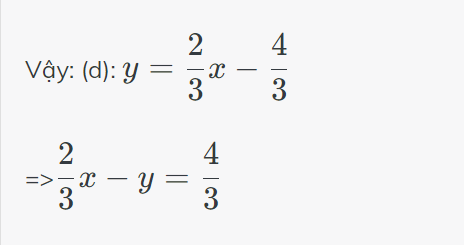
Vậy: Phương trình bậc nhất hai ẩn cần tìm là \(\dfrac{2}{3}x-y=\dfrac{4}{3}\)
Cho 2 số 13 và 18. Tìm phương trình bậc nhất 2 ẩn có hệ số của biến bậc cao nhất là 1 và nhận hai hệ số trên là nghiệm.
Cho x1, x2 là hai nghiệm của phương trình: x^2-2x-1=0.Hãy lập một phương trình bậc hai một ẩn có hại nghiệm là x1+(x2)^2 và x2+(x1)^2
Phần trắc nghiệm
Nội dung câu hỏi 1
Phương trình nào sau đây là phương trình bậc nhất hai ẩn:
A. 2 x 2 - 3x + 1 = 0
B.-2x = 4
C. 2x + 3y = 7
D. 1/x + y = 3
Phần trắc nghiệm
Nội dung câu hỏi 1
Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
A.xy + y = 5
B.3x - 2y = 0
C.x + xy = 2
D.x + y = xy
Cho phương trình bậc hai (ẩn ): x 2 - (m + 1)x + m – 2 = 0
a) Tìm m để phương trình có hai nghiệm phân biệt x 1 và x 2 .
Nếu tìm thấy hai nghiệm phân biệt của một hệ hai phương trình bậc nhất hai ẩn (nghĩa là hai nghiệm được biểu diễn bởi hai điểm phân biệt) thì ta có thể nói gì về số nghiệm của hệ phương trình đó? Vì sao?
Nếu tìm thấy hai nghiệm phân biệt của một hệ hai phương trình bậc nhất hai ẩn (nghĩa là hai nghiệm được biểu diễn bởi hai điểm phân biệt) thì ta có thể nói gì về số nghiệm của hệ phương trình đó? Vì sao?
Bạn Nga nhận xét: Hai hệ phương trình bậc nhất hai ẩn vô nghiệm thì luôn tương đương với nhau.
Bạn Phương khẳng định: Hai hệ phương trình bậc nhất hai ẩn cùng có vô số nghiệm thì cũng luôn tương đương với nhau.
Theo em, các ý kiến đó đúng hay sai? Vì sao? (Có thể cho một ví dụ hoặc minh họa bằng đồ thị).
Cặp số (x; y) = (1; 3) là nghiệm của hệ phương trình bậc nhất hai ẩn nào trong các hệ phương trình sau:
A. x - y = - 2 x + y = 4
B. 2 x - y = 0 x + y = 4
C. 2 x + y = 4 x + y = 4
D. x 2 + y 2 = 10 x - y = 2
Cặp số (x; y) = (1; 3) là nghiệm của hệ phương trình bậc nhất hai ẩn nào trong các hệ phương trình sau:
A. x − y = − 2 x + y = 4
B. 2 x − y = 0 x + y = 4
C. x + y = 4 2 x + y = 4
D. x 2 + y 2 = 10 x − y = 2