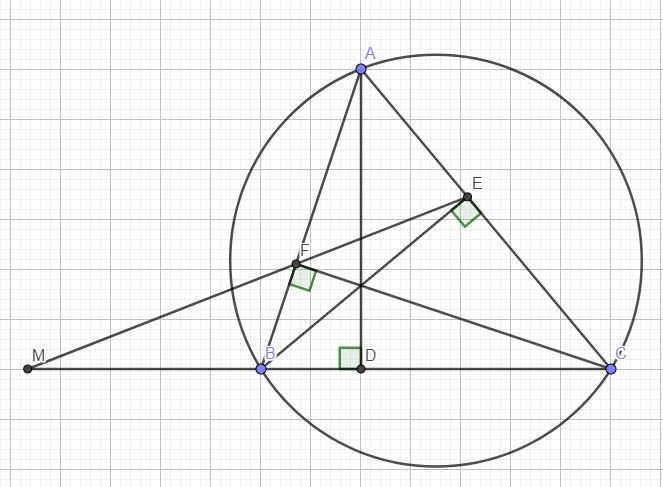
a.
Do BE, CF là các đường cao nên \(\widehat{BFC}=\widehat{BEC}=90^0\)
\(\Rightarrow E,F\) cùng nhìn BC dưới 1 góc vuông nên thứ giác BFEC nội tiếp
b.
Do BFEC nội tiếp \(\Rightarrow\widehat{BFE}+\widehat{MCE}=180^0\)
Mà \(\widehat{BFE}+\widehat{MFB}=180^0\) (kề bù)
\(\Rightarrow\widehat{MFB}=\widehat{MCE}\)
Xét hai tam giác MFB và MCE có:
\(\left\{{}\begin{matrix}\widehat{FMB}-chung\\\widehat{MFB}=\widehat{MCE}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta MFB\sim\Delta MCE\left(g.g\right)\)
\(\Rightarrow\dfrac{MF}{MC}=\dfrac{MB}{ME}\Rightarrow MF.ME=MB.MC\)
Đúng 1
Bình luận (0)