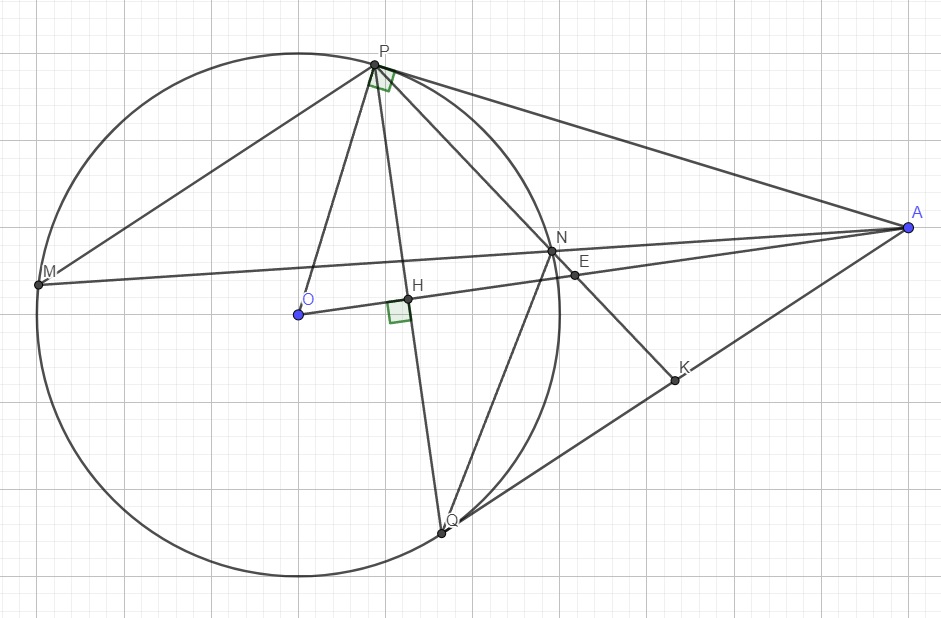
a.
Do AP, AQ là các tiếp tuyến \(\Rightarrow\widehat{APO}=\widehat{AQO}=90^0\)
\(\Rightarrow\) P, Q cùng nhìn AO dưới 1 góc vuông nên APOQ nội tiếp
b.
Theo t/c 2 tiếp tuyến cắt nhau: \(AP=AQ\)
Đồng thời \(OP=OQ=R\)
\(\Rightarrow OA\) là trung trực PQ \(\Rightarrow OA\perp PQ\) tại H
Áp dụng hệ thức lượng trong tam giác vuông OPA với đường cao PH:
\(AP^2=AH.AO\) (1)
Xét hai tam giác APN và AMP có:
\(\left\{{}\begin{matrix}\widehat{PAN}-chung\\\widehat{APN}=\widehat{AMP}\left(\text{cùng chắn PN}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta APN\sim\Delta AMP\left(g.g\right)\)
\(\Rightarrow\dfrac{AP}{AM}=\dfrac{AN}{AP}\Rightarrow AP^2=AM.AN\) (2)
(1);(2) \(\Rightarrow AM.AN=AH.AO\)
c.
Do PM song song AQ (gt) \(\Rightarrow\widehat{PMN}=\widehat{KAN}\) (so le trong)
Mà \(\widehat{PMN}=\widehat{KPA}\) (cùng chắn PN)
\(\Rightarrow\widehat{KAN}=\widehat{KPA}\)
Xét 2 tam giác KAN và KPA có:
\(\left\{{}\begin{matrix}\widehat{KAN}=\widehat{KPA}\left(cmt\right)\\\widehat{NKA}-chung\end{matrix}\right.\)
\(\Rightarrow\Delta KAN\sim\Delta KPA\left(g.g\right)\)
\(\Rightarrow\dfrac{KA}{KP}=\dfrac{KN}{KA}\Rightarrow KA^2=KN.KP\)
d.
Xét hai tam giác PQK và QNK có:
\(\left\{{}\begin{matrix}\widehat{QPK}=\widehat{NQK}\left(\text{cùng chắn QN}\right)\\\widehat{PKQ}-chung\end{matrix}\right.\)
\(\Rightarrow\Delta PQK\sim\Delta QNK\left(g.g\right)\)
\(\Rightarrow\dfrac{KP}{QK}=\dfrac{QK}{KN}\Rightarrow QK^2=KN.KP\)
Kết hợp câu c \(\Rightarrow QK^2=KA^2\Rightarrow QK=KA\)
Hay K là trung điểm AQ
Lại có theo cm câu b có OA là trung trực PQ \(\Rightarrow\) H là trung điểm PQ
\(\Rightarrow E\) là giao điểm 2 đường trung tuyến PK, AH của tam giác APQ nên E là trọng tâm tam giác APQ
\(\Rightarrow\dfrac{EK}{EP}=\dfrac{1}{2}\) (theo t/c trọng tâm)