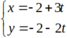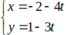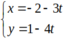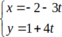
Ta có: A là giao điểm của AB và AD. Do đó, tọa độ A là nghiệm của hệ phương trình:
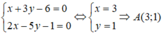
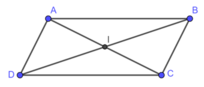
Hình bình hành ABCD có tâm I nên I là trung điểm của AC và BD ⇒ C(-1;3)
Đường thẳng BC đi qua C và song song với AD
Vì BC song song với AD nên BC có dạng: 2x - 5y + c = 0, (c ≠ -1)
Vì C thuộc BC nên: 2.(-1) - 5.3 + c = 0 ⇒ c = 17(tm)
Vậy phương trình đường thẳng BC là: 2x - 5y + 17 = 0
Đường thẳng DC đi qua C và song song với AB
Vì DC song song với AB nên DC có dạng: x + 3y + c = 0, (c ≠ -6)
Vì C thuộc DC nên: -1 + 3.3 + c = 0 ⇒ c = -8(tm)
Vậy phương trình đường thẳng DC là: x + 3y - 8 = 0