Chọn A
Thay tọa độ hai điểm A (3;1;0), B (-9;4;9) vào vế trái phương trình mặt phẳng (P), ta có
2. 3-1+0+1=6 > 0 và 2. (-9)-4+9+1 = -12 < 0.
Nên suy ra, hai điểm A, B nằm khác phía với mặt phẳng (P).
Gọi A' (-1;3;-2) là điểm đối xứng với điểm A qua mặt phẳng (P). Ta có
![]()
Dấu “=” xảy ra khi và chỉ khi A', B, I thẳng hàng và I nằm ngoài đoạn A'B. Suy ra I là giao điểm của đường thẳng A'B và mặt phẳng (P).
Ta có ![]() , nên suy ra phương trình đường thẳng A'B là
, nên suy ra phương trình đường thẳng A'B là 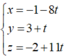 .
.
Tọa độ điểm I là nghiệm của hệ phương trình
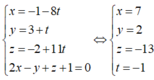
Vậy I (7;2;13) nên a+b+c=7+2+ (-13)=-4.

