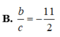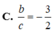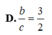Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto làm vectơ chỉ phương và song song với mặt phẳng (P): 2x+y+z=0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng:
A. 15
B. 13
C. 16
D. 14
Chọn A
Gọi (Q) là mặt phẳng đi qua M (2;2; -3) và song song với mặt phẳng (P).
Suy ra (Q):2x+y+z-3=0.
Do Δ // (P) nên Δ ⊂ (Q)).
D (N, Δ) đạt giá trị nhỏ nhất ó Δ đi qua N', với N' là hình chiếu của N lên (Q).
Gọi d là đường thẳng đi qua N và vuông góc (P), 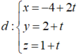
Ta có N’ ∈ d => N' (-4+2t;2+t;1+t); N’ ∈ (Q) => t = 4/3 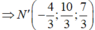
![]() cùng phương
cùng phương 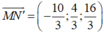
Do |a|, |b| nguyên tố cùng nhau nên chọn ![]()
Vậy |a| + |b| + |c| = 15.