Đáp án C
Cách giải:
Gọi tọa độ các giao điểm : A(a;0;0), B(0;b;0), C(0;0;c) (a;b;c ≠ 0)
Khi đó phương trình mặt phẳng (P) có dạng đoạn chắn: x a + y b + z c = 1
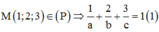
Vì OA = 2OB = 3OC > 0 nên |a| = 2|b| = 3|c| > 0

TH1: a = 2b = 3c

![]()
TH2: a = – 2b = 3c
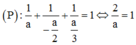
![]()
TH3: a = 2b = –3c
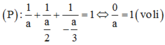
TH4: –a = 2b = –3c
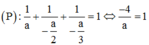
![]()
Vậy có 3 mặt phẳng (P) thỏa mãn yêu cầu đề bài

