[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part 2) ]
|-----------------------------------------------------------------------------|

#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS
(1) Phần số học
+ Số nguyên tố, phân tích một số ra thừa số nguyên tố
- Ở cấp THCS ta cần nắm và hiểu rõ về số nguyên tố
Số nguyên tố là số tự nhiên khác 1 và chia hết cho 1 và chia hết cho chính nó
VD: \(3,5,7,11,13,17,19,23,29,...\)
- Cách phân tích 1 số ra thừa số nguyên tố
Bước 1: Nhìn sơ quát số và nhẩm xem số đó chia hết cho 2,3,5 hay 7 không
Bước 2: Xét thương nếu thương không phải số nguyên tố thì tiếp tục phân tích
Bước 3: Tiếp tục phân tích thương dần đến kết quả cuối cùng là 1 số nguyên tố
VD: Phân tích số 35
Ta có: 35 = 7 x 5
+ Ước, bội, ước chung lớn nhất, bội chung nhỏ nhất
- Tập hợp các số mà số đó chia hết được gọi là ước
Được kí hiệu là Ư(x)
- Tập hợp các số chia hết cho số đó được gọi là bội
Được kí hiệu là B(x)
VD: Ư(10)\(=\left\{1;2;5;10\right\}\)
\(B\left(10\right)=\left\{0;10;20;30;40;50;...\right\}\)
- Ước chung là tập hợp ước của số này mà cũng là ước của số kia
Được kí hiệu là: ƯC(x;y)
- Bội chung là tập hợp bội của số này mà cũng là bội của số kia
Được kí hiệu là BC(x;y)
VD: \(Ư\left(12\right)=\left\{1;2;3;4;6;12\right\}\)
\(Ư\left(15\right)=\left\{1;3;5;15\right\}\)
\(\RightarrowƯC\left(12;15\right)=\left\{1;3\right\}\)
\(B\left(9\right)=\left\{0;9;18;27;36;54;...\right\}\)
\(B\left(3\right)=\left\{0;3;6;9;12;15;18;21;24;27;...\right\}\)
\(\Rightarrow BC\left(9;3\right)=\left\{0;9;18;27;..\right\}\)
- Ước chung lớn nhất là ước của số này cũng là ước của số kia nhưng đó là ước chung lớn nhất
Được kí hiệu là: ƯCLN
- Bội nhung nhỏ nhất là bội của số này cũng là bội của số kia nhưng đó là bội chung nhỏ nhất
Được kí hiệu là: BCNN
+ Số hữu tỉ, vô tỉ, số thập phân hữu hạn, vô hạng tuần hoàn, giá trị tuyệt đối
- Số hữu tỉ được biểu diễn dưới dạng \(\dfrac{a}{b}\left(a,b\in Z;b\ne0\right)\)
Tập hợp các số hữu tỉ được kí hiệu là tập hợp Q
- Số thập phân hữu hạn là số hữu tỉ tối giản không có ước nguyên tố khác 2 và 5
VD: \(\dfrac{1}{5};\dfrac{2}{5};\dfrac{5}{2};...\)
- Số thập phân vô hạn tuần hoàn là số hữu tỉ có ước nguyên tố khác 2,5
VD: \(\dfrac{3}{7};\dfrac{1}{6};\dfrac{1}{9};\dfrac{5}{7};...\)
- Cách công trừ nhân chia các số hữu tỉ:
Cộng số hữu tỉ:
\(\dfrac{a}{m}+\dfrac{b}{m}=\dfrac{a+b}{m}\)
Trừ số hữu tỉ:
\(\dfrac{a}{m}-\dfrac{b}{m}=\dfrac{a-b}{m}\)
Nhân số hữu tỉ:
\(\dfrac{a}{n}\cdot\dfrac{b}{m}=\dfrac{a\cdot b}{m\cdot n}\)
Chia số hũu tỉ:
\(\dfrac{a}{n}:\dfrac{b}{m}=\dfrac{a}{n}\cdot\dfrac{m}{b}=\dfrac{a\cdot m}{n\cdot b}\)
- Tính giá trị tuyệt đối của 1 số hữu tỉ:
\(\left\{{}\begin{matrix}khi:x\ge0\Rightarrow\left|x\right|=x\\khi:x< 0\Rightarrow\left|x\right|=-x\end{matrix}\right.\)
VD: \(\left|-5\right|=-\left(-5\right)=5\left(-5< 0\right)\)
\(\left|2\right|=2\left(2>0\right)\)
(2) Phần hình học
+ Một đường thẳng cắt 2 đường thẳng song song, hai góc so le trong, đồng vị, trong cùng phía
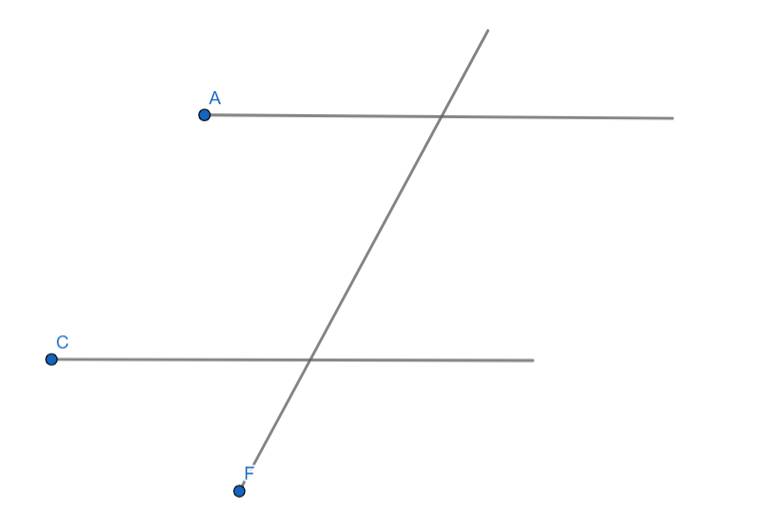
Lúc này ta có: \(A//C\) và \(F\) cắt \(A,C\)
Khi 1 đường thẳng cắt 2 đường thẳng song song sẽ tạp ra các cặp góc: so le trong, đồng vị, trong cùng phía
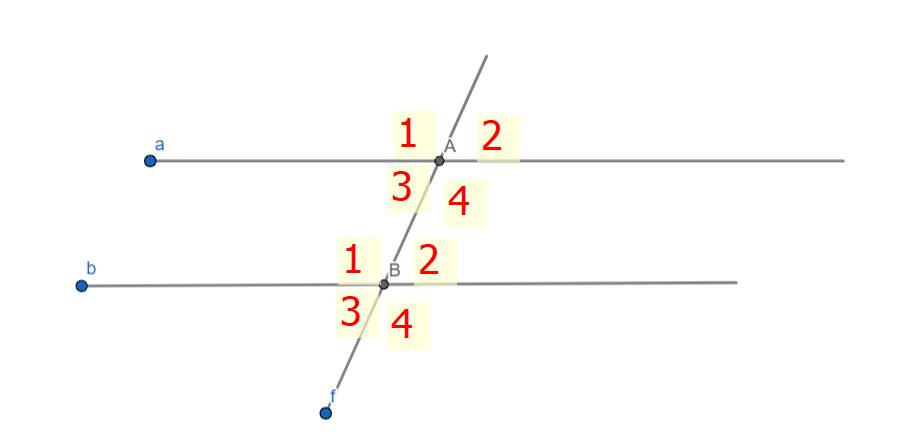
Khai niệm:
Hai góc đồng vị là 2 góc có cùng vị trí trong hai đường thẳng song song bị cắt bởi 1 đường thẳng
- Hai góc đồng vị có cùng số đo với nhau
VD: hai góc đồng vị trong hình:
\(\left(\widehat{A_1};\widehat{B_1}\right);\left(\widehat{A_2};\widehat{B_2}\right);\left(\widehat{A_3};\widehat{B_3}\right);\left(\widehat{A_4};\widehat{B_4}\right)\)
Hai góc so le trong là so le với nhau trong hai đường thẳng song song bị cắt bởi 1 đường thẳng
- Hai góc so le trong có cùng số đo với nhau
VD: hai góc so le trong ở trong hình: \(\left(\widehat{A_3};\widehat{B_2}\right);\left(\widehat{A_4};\widehat{B_1}\right)\)
Hai góc trong cùng phía là hai góc này bên trong 2 đường thẳng và cùng 1 phía trong hai đường thẳng song song bị cắt bởi 1 đường thẳng
- Hai góc trong cùng phía có tổng số đo là 180o
VD: hai góc trong cùng phía trong hình là:
\(\left(\widehat{A_3};\widehat{B_1}\right);\left(\widehat{A};\widehat{B_2}\right)\)
+ Diện tích hình chữ nhật hình vuông, hình tam giác, hình thang; hình bình hành; hình thoi,....
Với:
\(a\): cạnh đáy (chiều dài)
\(b\) :cạnh đáy lớn (chiều rộng)
\(h\): là chiều cao
\(d\): là đường chéo
- Diện tích hình chữ nhật:
\(S=a\times b\)
- Diện tích hình vuông:
\(S=a\times a=a^2\)
- Diện tích hình tam giác:
\(S=\dfrac{1}{2}\times a\times h\)
- Diện tích hình thang:
\(S=\dfrac{a+b}{2}\times h\)
- Diện tích hình bình hành:
\(S=a\times h\)
- Diện tích hình thôi:
\(S=\dfrac{d_1\times d_2}{2}\)
+ Diện tích xung quanh, diện tích toàn phần, thể tích hình hộp chữ nhật, hình lập phương
Với:
\(a\): cạnh (chiều rộng)
\(b\): chiều dài
\(h\): chiều cao
- Diện tích xung quanh của hình hộp chữ nhật:
\(S_{xq}=\left(a+b\right)\times2\times h\)
- Diện tích toàn phần của hình hộp chữ nhật:
\(S_{tp}=S_{xq}+S_đ\times2=\left(a+b\right)\times2\times h+a\times b\times2\)
- Thể tích hình hộp chữ nhật:
\(V=a\times b\times h\)
- Diện tích xung quanh hình lập phương:
\(S_{xq}=\left(a+a\right)\times2\times a=4a^2\)
- Diện tích toàn phần của hình lập phương là:
\(S_{tp}=S_{xq}+S_đ\times2=4a^2+2a^2=6a^2\)
- Thể tích hình lập phương là:
\(V=a\times a\times a=a^3\)
__________________________________________
*Cách học môn toán không bị nhàm chán và thú vi cần biết các tips sau: *
- Không được học liên tiếp 2 - 3 giờ sẽ khiến cho cơ thể mệt mỏi buồn ngủ không hiệu quả
- Để không bị mất gốc thì nên học toàn chú trọng vào các ý chính (VD: ghi nhớ, các điều mà thầy cô lưu ý học)
- Không cần thuộc lòng quan trọng là biết vận dụng vào bài toán
- Cần lưu ý các kiến thức toán cở cấp độ của mình (tiểu học, THCS, THPT)
- Phối hợp việc học toán và việc giải trí tránh bị nhàm chán mất tinh thần
- ....
Các bạn hay anh chị có các tips học toán thú vị hơn mong anh chị bình luận ở đây nhé (trân trọng)
(* Nếu trong part 1 này có gì thiếu sót thì mong các anh chị và các bạn góp ý với mình nhé mình sẽ cải thiện điều đó trong các part tới ạ *)
Uii, toàn mấy phần iemm đang cần luôn nè :>>
phần hình e toàn quên công thức
Nhận ngay giải thưởng 1 coin khi góp ý cho mình tỏng các part sau nhé và có thể bổ sung thêm các tips học toán
Bạn ơi, mình có một số góp ý như sau:
- Phần số nguyên tố nên thêm điều kiện là khác 0
- Phần ước và bội thì cần bổ sung thêm trong tập ước các ước là số âm
+ VD: \(Ư\left(10\right)=\left\{1;2;5;10;-1;-2;-5;-10\right\}\)
- Sửa các lỗi chính tả nhé
(Đây là ý kiến riêng của mình. Trân trọng!)
Mình bổ sung nha.
Diện tích tam giác vuông : \(S=\dfrac{a.b}{2}\)
Toàn mấy phần e đang cần anh ạ :) Cuối cùng cũng có phần Số nguyên tố .-. Mấy cái kia e cũng sắp học nữa, hay hay .-.
Tips học toán nè a:
- Sử dụng sơ đồ tư duy, takenotes,...
- Ôn lại nhiều lần các khái niệm, kiến thức,...
- Tìm và làm đi làm lại dạng bài mình còn yếu
- KHÔNG BIẾT PHẢI HỎI, KHÔNG CHE DỐT
*tips e đã sử dụng nên là em gửi vào đây, có thể không phù hợp với các a/c ạ*
Mình có các tip học toán vô cùng siêu đẳng:
- Sơ đồ tư duy
- Sử dụng trí nhớ siêu đẳng cái này mình nói thêm là có hệ thống số và chữ nhé
- Dùng kỹ thuật gợi nhớ
- Dùng hệ thống trí nhớ