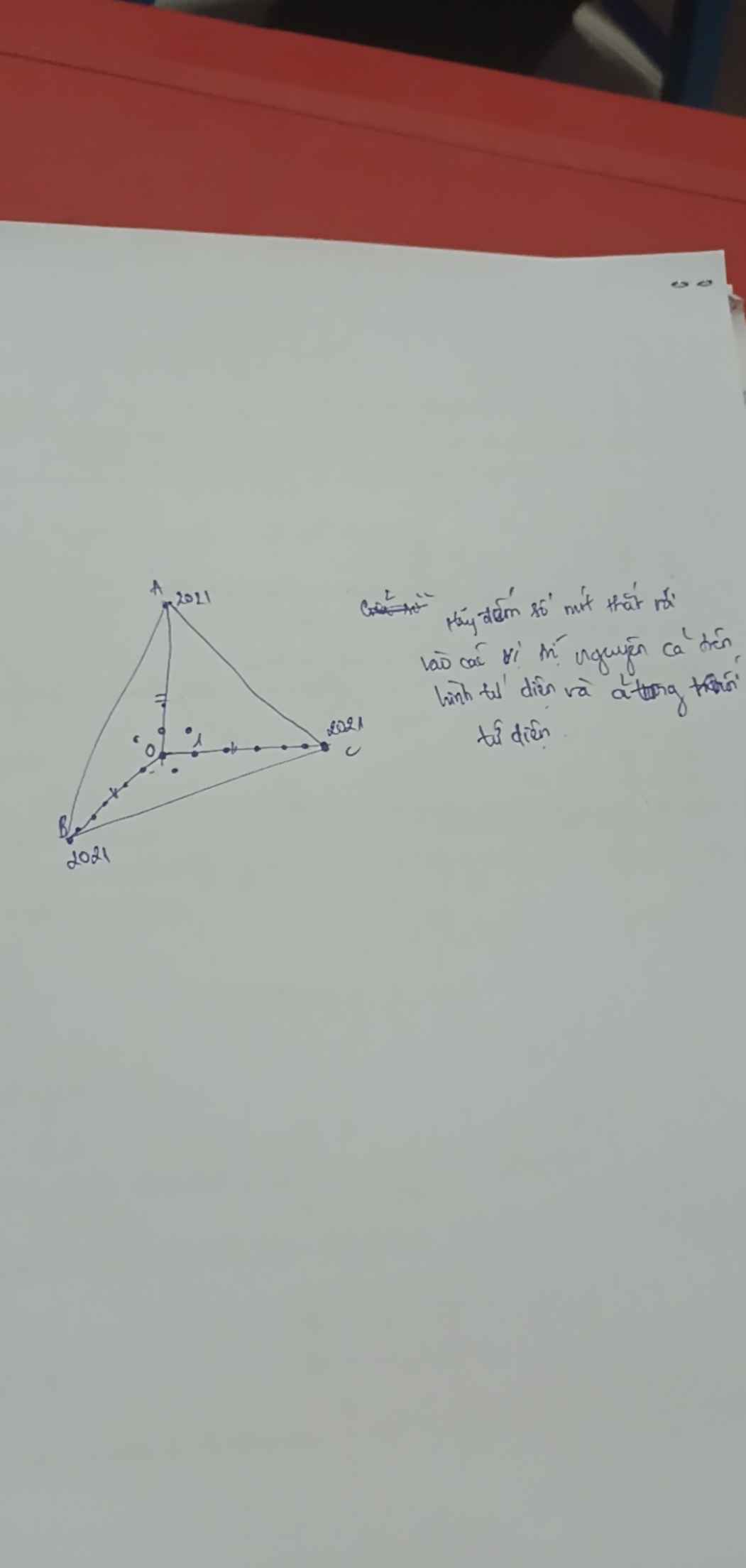
Xét khai triển:
\(2^{2021}=\left(1+1\right)^{2021}=C_{2021}^0+C_{2021}^1+...+C_{2021}^{2020}+C_{2021}^{2021}\) (1)
\(0=\left(1-1\right)^{2021}=C_{2021}^0-C_{2021}^1+C_{2021}^2+...+C_{2021}^{2020}-C_{2021}^{2021}\) (2)
Trừ vế cho vế (1) và (2):
\(2^{2021}=2.C_{2021}^1+2.C_{2021}^3+...+2C_{2021}^{2021}\)
\(\Rightarrow C_{2021}^1+C_{2021}^3+...+C_{2021}^{2019}+C_{2021}^{2021}=\dfrac{2^{2021}}{2}=2^{2020}\)
\(\Rightarrow C_{2021}^1+C_{2021}^3+...+C_{2021}^{2019}+1=2^{2020}\)
\(\Rightarrow C_{2021}^1+C_{2021}^3+...+C_{2021}^{2019}=2^{2020}-1\)