Bài 1. Tính tổng:dfrac{1}{2}+dfrac{1}{4}+dfrac{1}{8}+dfrac{1}{16}+dfrac{1}{32}Bài 2. Hai số thập phân có tổng bằng 271,48. Biết rằng nếu dời dấu phẩy của số thứ nhất sang trái một hàng ta được số thứ hai. Tìm số thứ nhất.Bài 3. Tìm số nhỏ nhất có 3 chữ số chia hết cho 5 và tổng các chữ số của số đó bằng 10.Bài 4. Có 35 học sinh đứng thành một hàng. Họ bắt đầu điểm danh theo thứ tự 1, 2, 3 ... kể từ bên trái sang, và Nam có số thứ tự là 13. Hỏi nếu họ điểm danh kể từ bên phải sang thì Nam sẽ có s...
Đọc tiếp
Bài 1. Tính tổng:
\(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}\)
Bài 2. Hai số thập phân có tổng bằng 271,48. Biết rằng nếu dời dấu phẩy của số thứ nhất sang trái một hàng ta được số thứ hai. Tìm số thứ nhất.
Bài 3. Tìm số nhỏ nhất có 3 chữ số chia hết cho 5 và tổng các chữ số của số đó bằng 10.
Bài 4. Có 35 học sinh đứng thành một hàng. Họ bắt đầu điểm danh theo thứ tự 1, 2, 3 ... kể từ bên trái sang, và Nam có số thứ tự là 13. Hỏi nếu họ điểm danh kể từ bên phải sang thì Nam sẽ có số thứ tự là bao nhiêu?
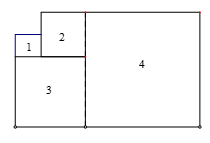
Bài 5. Bốn hình 1, 2, 3, 4 đều là các hình vuông. Độ dài cạnh hình 1 và hình 3 lần lượt là 20cm và 60cm. Tính độ dài cạnh hình 4.
Bài 6. Tổng 2 số chẵn bằng 480. Tìm số chẵn lớn hơn, biết giữa 2 số chẵn đó có đúng 6 số lẻ liên tiếp.
Bài 7. Tính tổng tất cả các số tự nhiên nhỏ hơn 300 mà chia hết cho 5.
Bài 8. Trong dịp Tết vừa qua, bạn Chi đã được mừng tuổi 1 số tiền. Bạn đã mua đồ chơi hết 1/3 số tiền, sau đó ủng hộ 1/3 số tiền còn lại vào quỹ từ thiện của trường. Cuối cùng bạn Chi còn lại 400 000 đồng. Hỏi tổng số tiền Chi được mừng tuổi là bao nhiêu?
Bài 9. Có một cốc nước đường 340g trong đó lượng đường chiếm tỉ lệ 5%. Hỏi cần phải cho thêm bao nhiêu gam đường vào cốc nước đường đó để được một cốc nước đường mới có tỉ lệ phần trăm đường là 15%?
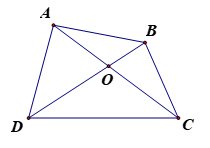
Bài 10. Cho tứ giác ABCD có 2 đường chéo cắt nhau tại O. Biết diện tích các tam giác AOB, AOD và COD lần lượt bằng 12cm2; 15cm2 và 18cm2. Tính diện tích tứ giác ABCD
mik cần đáp án thôi ạ giúp mik vs mik cần gấp!!!





